pymc.ZeroInflatedPoisson

class pymc.ZeroInflatedPoisson(name, psi, mu, **kwargs)

Zero-inflated Poisson log-likelihood.

Often used to model the number of events occurring in a fixed period of time when the times at which events occur are independent. The pmf of this distribution is

\[\begin{split}f(x \mid \psi, \mu) = \left\{ \begin{array}{l} (1-\psi) + \psi e^{-\mu}, \text{if } x = 0 \\ \psi \frac{e^{-\mu}\mu^x}{x!}, \text{if } x=1,2,3,\ldots \end{array} \right.\end{split}\]

(Source code, png, hires.png, pdf)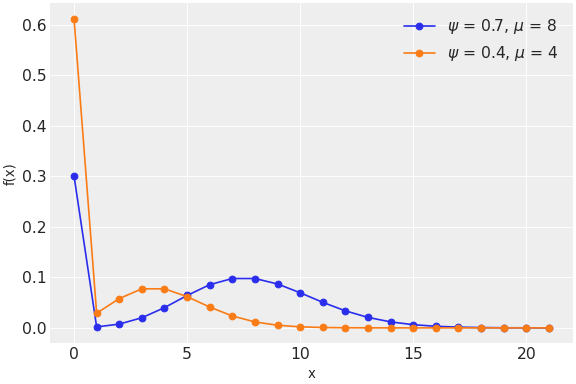

Support	\(x \in \mathbb{N}_0\)
Mean	\(\psi\mu\)
Variance	\(\mu + \frac{1-\psi}{\psi}\mu^2\)

Parameters:

psitensor_like of float

Expected proportion of Poisson draws (0 < psi < 1)

mutensor_like of float

Expected number of occurrences during the given interval (mu >= 0).

Methods

ZeroInflatedPoisson.dist(psi, mu, **kwargs)