pymc.Pareto#
- class pymc.Pareto(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[source]#
Pareto log-likelihood.
Often used to characterize wealth distribution, or other examples of the 80/20 rule.
The pdf of this distribution is
\[f(x \mid \alpha, m) = \frac{\alpha m^{\alpha}}{x^{\alpha+1}}\](
Source code,png,hires.png,pdf)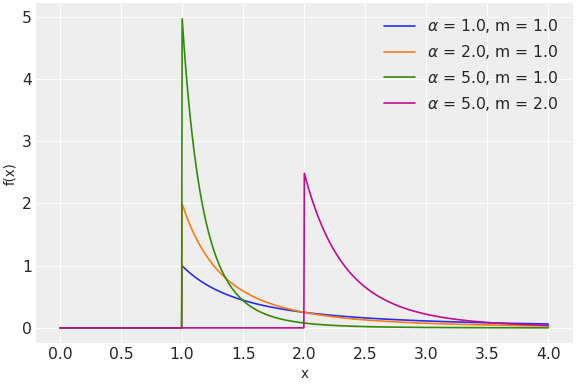
Support
\(x \in [m, \infty)\)
Mean
\(\dfrac{\alpha m}{\alpha - 1}\) for \(\alpha \ge 1\)
Variance
\(\dfrac{m \alpha}{(\alpha - 1)^2 (\alpha - 2)}\) for \(\alpha > 2\)
- Parameters:
- alphatensor_like of
float Shape parameter (alpha > 0).
- mtensor_like of
float Scale parameter (m > 0).
- alphatensor_like of
Methods
Pareto.dist(alpha, m, **kwargs)Creates a tensor variable corresponding to the cls distribution.