pymc.ExGaussian#
- class pymc.ExGaussian(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[source]#
Exponentially modified Gaussian log-likelihood.
Results from the convolution of a normal distribution with an exponential distribution.
The pdf of this distribution is
\[f(x \mid \mu, \sigma, \tau) = \frac{1}{\nu}\; \exp\left\{\frac{\mu-x}{\nu}+\frac{\sigma^2}{2\nu^2}\right\} \Phi\left(\frac{x-\mu}{\sigma}-\frac{\sigma}{\nu}\right)\]where \(\Phi\) is the cumulative distribution function of the standard normal distribution.
(
Source code,png,hires.png,pdf)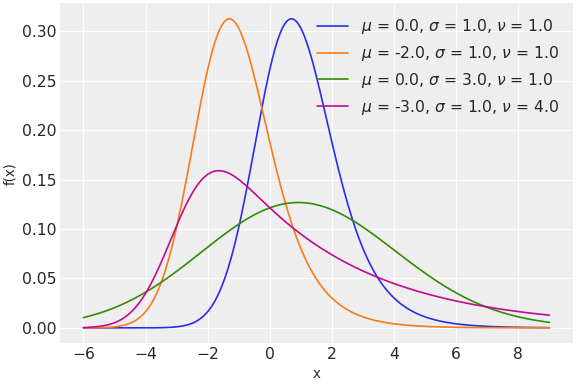
Support
\(x \in \mathbb{R}\)
Mean
\(\mu + \nu\)
Variance
\(\sigma^2 + \nu^2\)
- Parameters:
- mutensor_like of
float, default 0 Mean of the normal distribution.
- sigmatensor_like of
float Standard deviation of the normal distribution (sigma > 0).
- nutensor_like of
float Mean of the exponential distribution (nu > 0).
- mutensor_like of
References
[Rigby2005]Rigby R.A. and Stasinopoulos D.M. (2005). “Generalized additive models for location, scale and shape” Applied Statististics., 54, part 3, pp 507-554.
[Lacouture2008]Lacouture, Y. and Couseanou, D. (2008). “How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times”. Tutorials in Quantitative Methods for Psychology, Vol. 4, No. 1, pp 35-45.
Methods
ExGaussian.dist([mu, sigma, nu])Creates a tensor variable corresponding to the cls distribution.