pymc.HalfNormal#
- class pymc.HalfNormal(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[source]#
Half-normal log-likelihood.
The pdf of this distribution is
\[ \begin{align}\begin{aligned}f(x \mid \tau) = \sqrt{\frac{2\tau}{\pi}} \exp\left(\frac{-x^2 \tau}{2}\right)\\f(x \mid \sigma) = \sqrt{\frac{2}{\pi\sigma^2}} \exp\left(\frac{-x^2}{2\sigma^2}\right)\end{aligned}\end{align} \]Note
The parameters
sigma/tau(\(\sigma\)/\(\tau\)) refer to the standard deviation/precision of the unfolded normal distribution, for the standard deviation of the half-normal distribution, see below. For the half-normal, they are just two parameterisation \(\sigma^2 \equiv \frac{1}{\tau}\) of a scale parameter.(
Source code,png,hires.png,pdf)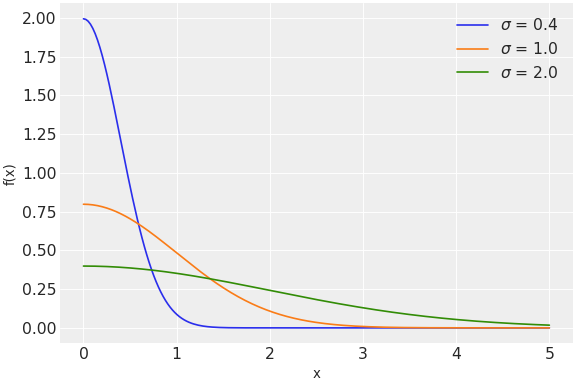
Support
\(x \in [0, \infty)\)
Mean
\(\sqrt{\dfrac{2}{\tau \pi}}\) or \(\dfrac{\sigma \sqrt{2}}{\sqrt{\pi}}\)
Variance
\(\dfrac{1}{\tau}\left(1 - \dfrac{2}{\pi}\right)\) or \(\sigma^2\left(1 - \dfrac{2}{\pi}\right)\)
- Parameters:
- sigmatensor_like of
float, optional Scale parameter \(\sigma\) (
sigma> 0) (only required iftauis not specified). Defaults to 1.- tautensor_like of
float, optional Precision \(\tau\) (tau > 0) (only required if sigma is not specified). Defaults to 1.
- sigmatensor_like of
Examples
with pm.Model(): x = pm.HalfNormal('x', sigma=10) with pm.Model(): x = pm.HalfNormal('x', tau=1/15)
Methods
HalfNormal.dist([sigma, tau])Creates a tensor variable corresponding to the cls distribution.