pymc.Gamma#
- class pymc.Gamma(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#
Gamma log-likelihood.
Represents the sum of alpha exponentially distributed random variables, each of which has rate beta.
The pdf of this distribution is
\[f(x \mid \alpha, \beta) = \frac{\beta^{\alpha}x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}\](
Source code,png,hires.png,pdf)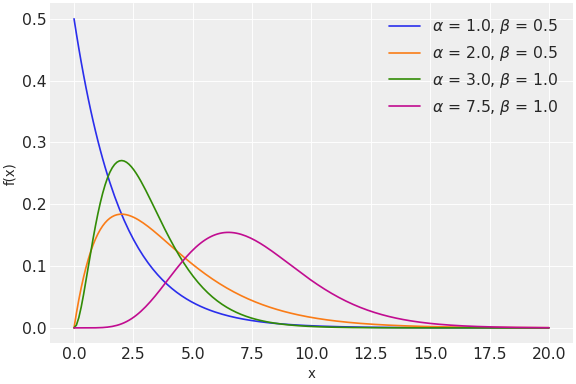
Support
\(x \in (0, \infty)\)
Mean
\(\dfrac{\alpha}{\beta}\)
Variance
\(\dfrac{\alpha}{\beta^2}\)
Gamma distribution can be parameterized either in terms of alpha and beta or mean and standard deviation. The link between the two parametrizations is given by
\[\begin{split}\alpha &= \frac{\mu^2}{\sigma^2} \\ \beta &= \frac{\mu}{\sigma^2}\end{split}\]- Parameters:
- alphatensor_like of
float, optional Shape parameter (alpha > 0).
- betatensor_like of
float, optional Rate parameter (beta > 0).
- mutensor_like of
float, optional Alternative shape parameter (mu > 0).
- sigmatensor_like of
float, optional Alternative scale parameter (sigma > 0).
- alphatensor_like of
Methods
Gamma.dist([alpha, beta, mu, sigma])Creates a tensor variable corresponding to the cls distribution.
