pymc.PolyaGamma#
- class pymc.PolyaGamma(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, **kwargs)[source]#
The Polya-Gamma distribution.
The distribution is parametrized by
h(shape parameter) andz(exponential tilting parameter). The pdf of this distribution is\[f(x \mid h, z) = cosh^h(\frac{z}{2})e^{-\frac{1}{2}xz^2}f(x \mid h, 0),\]where \(f(x \mid h, 0)\) is the pdf of a \(PG(h, 0)\) variable. Notice that the pdf of this distribution is expressed as an alternating-sign sum of inverse-Gaussian densities.
\[X = \Sigma_{k=1}^{\infty}\frac{Ga(h, 1)}{d_k},\]where \(d_k = 2(k - 0.5)^2\pi^2 + z^2/2\), \(Ga(h, 1)\) is a gamma random variable with shape parameter
hand scale parameter1.(
Source code,png,hires.png,pdf)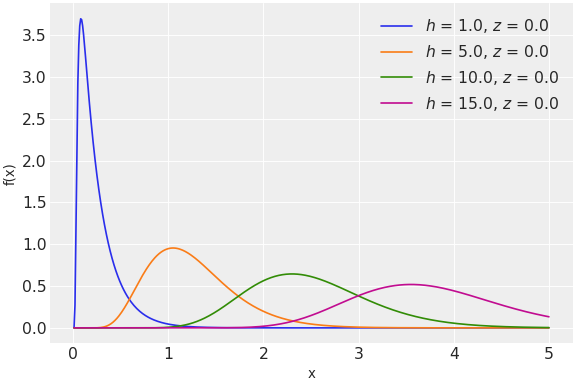
Support
\(x \in (0, \infty)\)
Mean
\(\dfrac{h}{4}\) if \(z=0\), \(\dfrac{tanh(z/2)h}{2z}\) otherwise.
Variance
\(0.041666688h\) if \(z=0\), \(\dfrac{h(sinh(z) - z)(1 - tanh^2(z/2))}{4z^3}\) otherwise.
- Parameters:
- htensor_like of
float, default 1 The shape parameter of the distribution (h > 0).
- ztensor_like of
float, default 0 The exponential tilting parameter of the distribution.
- htensor_like of
References
[1]Polson, Nicholas G., James G. Scott, and Jesse Windle. “Bayesian inference for logistic models using Pólya–Gamma latent variables.” Journal of the American statistical Association 108.504 (2013): 1339-1349.
[2]Windle, Jesse, Nicholas G. Polson, and James G. Scott. “Sampling Polya-Gamma random variates: alternate and approximate techniques.” arXiv preprint arXiv:1405.0506 (2014).
[3]Luc Devroye. “On exact simulation algorithms for some distributions related to Jacobi theta functions.” Statistics & Probability Letters, Volume 79, Issue 21, (2009): 2251-2259.
[4]Windle, J. (2013). Forecasting high-dimensional, time-varying variance-covariance matrices with high-frequency data and sampling Pólya-Gamma random variates for posterior distributions derived from logistic likelihoods.(PhD thesis). Retrieved from http://hdl.handle.net/2152/21842
Examples
rng = np.random.default_rng() with pm.Model(): x = pm.PolyaGamma('x', h=1, z=5.5) with pm.Model(): x = pm.PolyaGamma('x', h=25, z=-2.3, rng=rng, size=(100, 5))
Methods
PolyaGamma.dist([h, z])Creates a tensor variable corresponding to the cls distribution.