pymc.LogNormal#

class pymc.LogNormal(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#

Log-normal log-likelihood.

Distribution of any random variable whose logarithm is normally distributed. A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many small independent factors.

Note: Class name Lognormal is deprecated, use LogNormal now!

The pdf of this distribution is

\[f(x \mid \mu, \tau) = \frac{1}{x} \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (\ln(x)-\mu)^2 \right\}\]

(Source code, png, hires.png, pdf)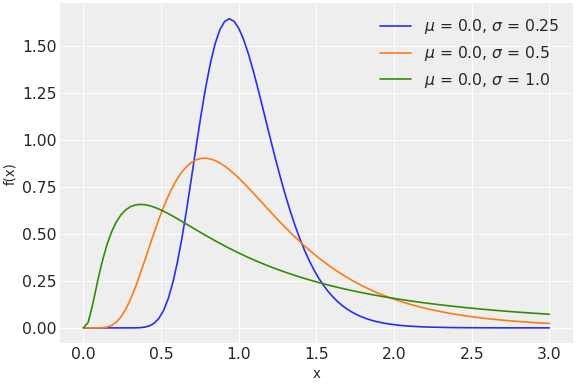

Support	\(x \in [0, \infty)\)
Mean	\(\exp\{\mu + \frac{1}{2\tau}\}\)
Variance	\((\exp\{\frac{1}{\tau}\} - 1) \times \exp\{2\mu + \frac{1}{\tau}\}\)

Parameters:

mutensor_like of float, default 0: Location parameter.
sigmatensor_like of float, optional: Standard deviation. (sigma > 0). (only required if tau is not specified). Defaults to 1.
tautensor_like of float, optional: Scale parameter (tau > 0). (only required if sigma is not specified). Defaults to 1.

Examples

# Example to show that we pass in only ``sigma`` or ``tau`` but not both.
with pm.Model():
    x = pm.LogNormal("x", mu=2, sigma=30)

with pm.Model():
    x = pm.LogNormal("x", mu=2, tau=1 / 100)

Methods

LogNormal.dist([mu, sigma, tau])

Creates a tensor variable corresponding to the cls distribution.