pymc.Wald

class pymc.Wald(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)

Wald log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \lambda) = \left(\frac{\lambda}{2\pi}\right)^{1/2} x^{-3/2} \exp\left\{ -\frac{\lambda}{2x}\left(\frac{x-\mu}{\mu}\right)^2 \right\}\]

(Source code, png, hires.png, pdf)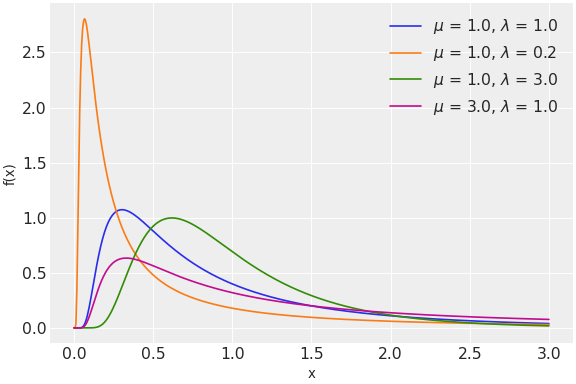

Support	\(x \in (0, \infty)\)
Mean	\(\mu\)
Variance	\(\dfrac{\mu^3}{\lambda}\)

Wald distribution can be parameterized either in terms of lam or phi. The link between the two parametrizations is given by

\[\phi = \dfrac{\lambda}{\mu}\]

Parameters:

mutensor_like of float, optional

Mean of the distribution (mu > 0).

lamtensor_like of float, optional

Relative precision (lam > 0).

phitensor_like of float, optional

Alternative shape parameter (phi > 0).

alphatensor_like of float, default 0

Shift/location parameter (alpha >= 0).

Notes

To instantiate the distribution specify any of the following

• only mu (in this case lam will be 1)

• mu and lam

• mu and phi

• lam and phi

References

[Tweedie1957]

Tweedie, M. C. K. (1957). Statistical Properties of Inverse Gaussian Distributions I. The Annals of Mathematical Statistics, Vol. 28, No. 2, pp. 362-377

[Michael1976]

Michael, J. R., Schucany, W. R. and Hass, R. W. (1976). Generating Random Variates Using Transformations with Multiple Roots. The American Statistician, Vol. 30, No. 2, pp. 88-90

[Giner2016]

Göknur Giner, Gordon K. Smyth (2016) statmod: Probability Calculations for the Inverse Gaussian Distribution

Methods

Wald.dist([mu, lam, phi, alpha])

Create a tensor variable corresponding to the cls distribution.