pymc.Rice

class pymc.Rice(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)

Rice distribution.

\[f(x\mid \nu ,\sigma )= {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),\]

(Source code, png, hires.png, pdf)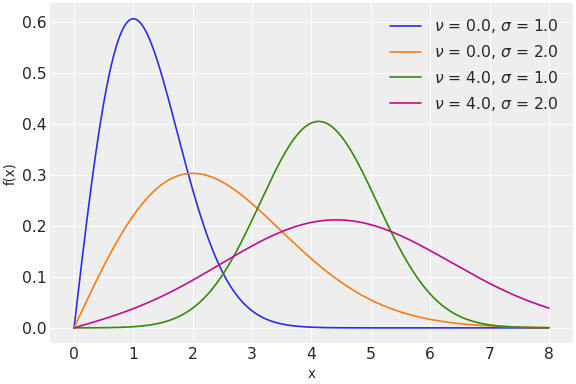

Support	\(x \in (0, \infty)\)
Mean	\(\sigma {\sqrt {\pi /2}}\,\,L_{{1/2}}(-\nu ^{2}/2\sigma ^{2})\)
Variance	\(2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{{1/2}}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)\)

Parameters:

nutensor_like of float, optional

Noncentrality parameter (only required if b is not specified).

sigmatensor_like of float, default 1

scale parameter.

btensor_like of float, optional

Shape parameter (alternative to nu, only required if nu is not specified).

Notes

The distribution \(\mathrm{Rice}\left(|\nu|,\sigma\right)\) is the distribution of \(R=\sqrt{X^2+Y^2}\) where \(X\sim N(\nu \cos{\theta}, \sigma^2)\), \(Y\sim N(\nu \sin{\theta}, \sigma^2)\) are independent and for any real \(\theta\).

The distribution is defined with either nu or b. The link between the two parametrizations is given by

\[b = \dfrac{\nu}{\sigma}\]

Methods

Rice.dist([nu, sigma, b])

Creates a tensor variable corresponding to the cls distribution.