pymc.DiscreteWeibull#
- class pymc.DiscreteWeibull(name, *args, **kwargs)[source]#
Discrete Weibull log-likelihood.
The discrete Weibull distribution is a flexible model of count data that can handle both over- and under-dispersion. The pmf of this distribution is
\[f(x \mid q, \beta) = q^{x^{\beta}} - q^{(x + 1)^{\beta}}\](
Source code,png,hires.png,pdf)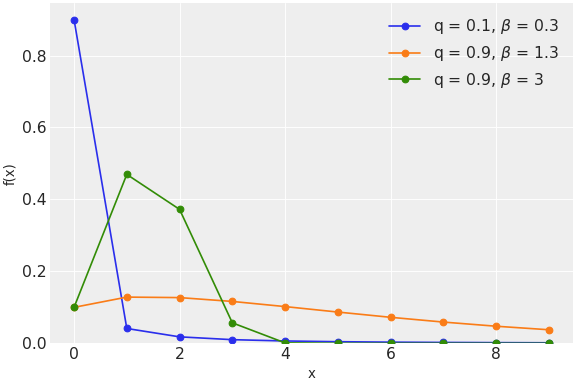
Support
\(x \in \mathbb{N}_0\)
Mean
\(\mu = \sum_{x = 1}^{\infty} q^{x^{\beta}}\)
Variance
\(2 \sum_{x = 1}^{\infty} x q^{x^{\beta}} - \mu - \mu^2\)
- Parameters:
- qtensor_like of
float Shape parameter (0 < q < 1).
- betatensor_like of
float Shape parameter (beta > 0).
- qtensor_like of
Methods
DiscreteWeibull.dist(q, beta, *args, **kwargs)Creates a tensor variable corresponding to the cls distribution.