pymc.HyperGeometric#
- class pymc.HyperGeometric(name, *args, **kwargs)[source]#
Discrete hypergeometric distribution.
The probability of \(x\) successes in a sequence of \(n\) bernoulli trials taken without replacement from a population of \(N\) objects, containing \(k\) good (or successful or Type I) objects. The pmf of this distribution is
\[f(x \mid N, n, k) = \frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}}\](
Source code,png,hires.png,pdf)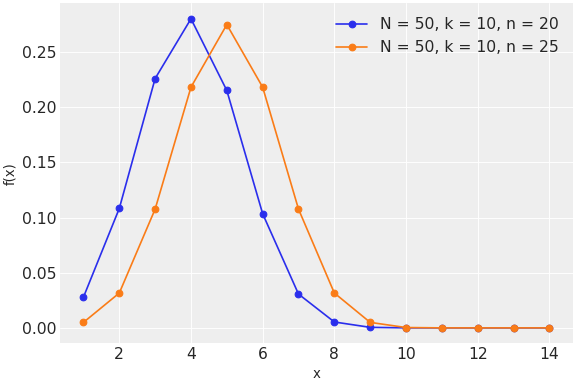
Support
\(x \in \left[\max(0, n - N + k), \min(k, n)\right]\)
Mean
\(\dfrac{nk}{N}\)
Variance
\(\dfrac{(N-n)nk(N-k)}{(N-1)N^2}\)
- Parameters:
- Ntensor_like of
int Total size of the population (N > 0)
- ktensor_like of
int Number of successful individuals in the population (0 <= k <= N)
- ntensor_like of
int Number of samples drawn from the population (0 <= n <= N)
- Ntensor_like of
Methods
HyperGeometric.dist(N, k, n, *args, **kwargs)Creates a tensor variable corresponding to the cls distribution.