Introduction to Variational Inference with PyMC#
The most common strategy for computing posterior quantities of Bayesian models is via sampling, particularly Markov chain Monte Carlo (MCMC) algorithms. While sampling algorithms and associated computing have continually improved in performance and efficiency, MCMC methods still scale poorly with data size, and become prohibitive for more than a few thousand observations. A more scalable alternative to sampling is variational inference (VI), which re-frames the problem of computing the posterior distribution as an optimization problem.
In PyMC, the variational inference API is focused on approximating posterior distributions through a suite of modern algorithms. Common use cases to which this module can be applied include:
Sampling from model posterior and computing arbitrary expressions
Conducting Monte Carlo approximation of expectation, variance, and other statistics
Removing symbolic dependence on PyMC random nodes and evaluate expressions (using
eval)Providing a bridge to arbitrary PyTensor code
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
import seaborn as sns
np.random.seed(42)
Distributional Approximations#
There are severa methods in statistics that use a simpler distribution to approximate a more complex distribution. Perhaps the best-known example is the Laplace (normal) approximation. This involves constructing a Taylor series of the target posterior, but retaining only the terms of quadratic order and using those to construct a multivariate normal approximation.
Similarly, variational inference is another distributional approximation method where, rather than leveraging a Taylor series, some class of approximating distribution is chosen and its parameters are optimized such that the resulting distribution is as close as possible to the posterior. In essence, VI is a deterministic approximation that places bounds on the density of interest, then uses opimization to choose from that bounded set.
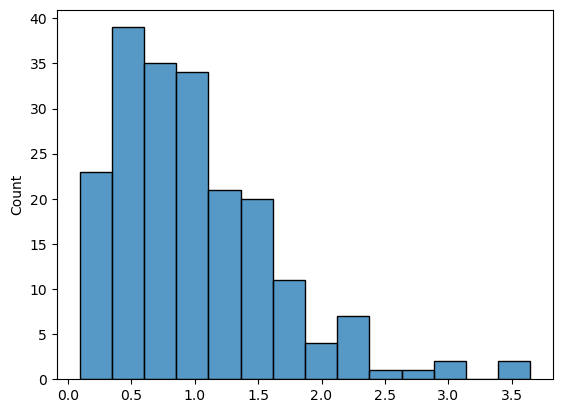
gamma_data = np.random.gamma(2, 0.5, size=200)
sns.histplot(gamma_data);
with pm.Model() as gamma_model:
alpha = pm.Exponential("alpha", 0.1)
beta = pm.Exponential("beta", 0.1)
y = pm.Gamma("y", alpha, beta, observed=gamma_data)
with gamma_model:
# mean_field = pm.fit()
mean_field = pm.fit(obj_optimizer=pm.adagrad_window(learning_rate=1e-2))
Finished [100%]: Average Loss = 169.87
with gamma_model:
trace = pm.sample()
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 3 seconds.
mean_field
<pymc.variational.approximations.MeanField at 0x7fca20419e50>
plt.plot(mean_field.hist);
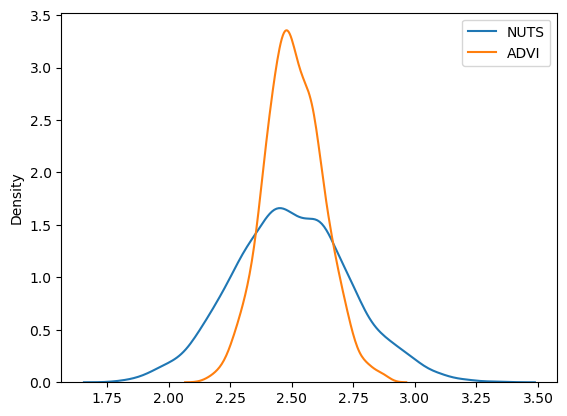
approx_sample = mean_field.sample(1000)
sns.kdeplot(trace.posterior["alpha"].values.flatten(), label="NUTS")
sns.kdeplot(approx_sample.posterior["alpha"].values.flatten(), label="ADVI")
plt.legend();
Basic setup#
We do not need complex models to play with the VI API; let’s begin with a simple mixture model:
w = np.array([0.2, 0.8])
mu = np.array([-0.3, 0.5])
sd = np.array([0.1, 0.1])
with pm.Model() as model:
x = pm.NormalMixture("x", w=w, mu=mu, sigma=sd)
x2 = x**2
sin_x = pm.math.sin(x)
We can’t compute analytical expectations for this model. However, we can obtain an approximation using Markov chain Monte Carlo methods; let’s use NUTS first.
To allow samples of the expressions to be saved, we need to wrap them in Deterministic objects:
with model:
pm.Deterministic("x2", x2)
pm.Deterministic("sin_x", sin_x)
with model:
trace = pm.sample(5000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [x]
Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 5 seconds.
az.plot_trace(trace);
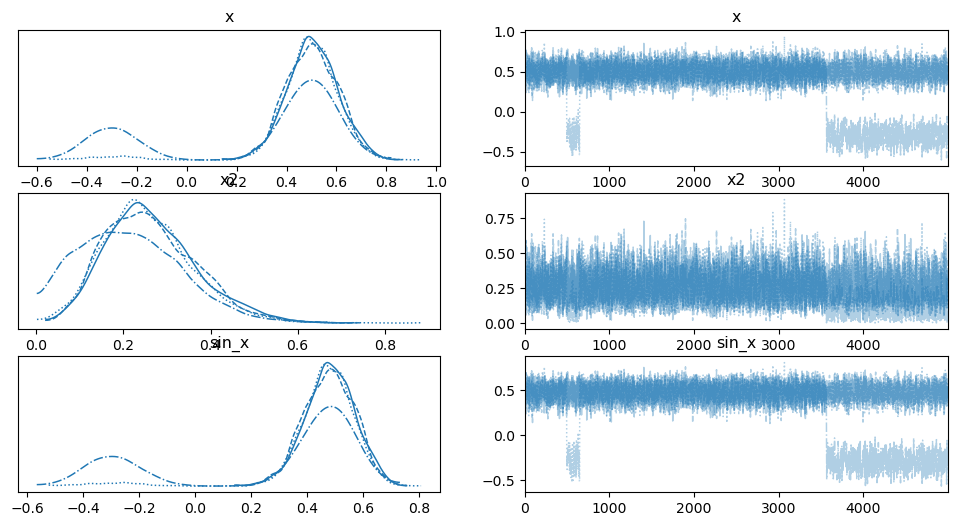
Above are traces for \(x^2\) and \(sin(x)\). We can see there is clear multi-modality in this model. One drawback, is that you need to know in advance what exactly you want to see in trace and wrap it with Deterministic.
The VI API takes an alternate approach: You obtain inference from model, then calculate expressions based on this model afterwards.
Let’s use the same model:
with pm.Model() as model:
x = pm.NormalMixture("x", w=w, mu=mu, sigma=sd)
x2 = x**2
sin_x = pm.math.sin(x)
Here we will use automatic differentiation variational inference (ADVI).
with model:
mean_field = pm.fit(method="advi")
Finished [100%]: Average Loss = 2.216
az.plot_posterior(mean_field.sample(1000), color="LightSeaGreen");
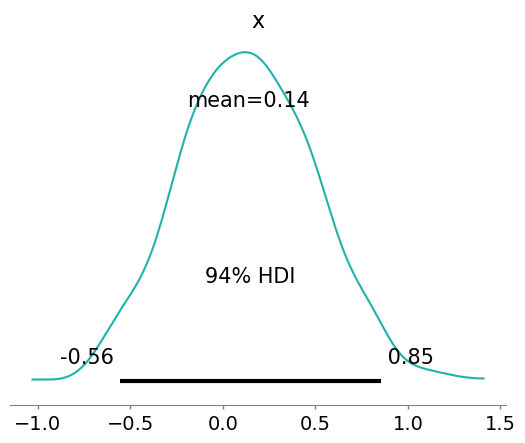
Notice that ADVI has failed to approximate the multimodal distribution, since it uses a Gaussian distribution that has a single mode.
Checking convergence#
Let’s use the default arguments for CheckParametersConvergence as they seem to be reasonable.
from pymc.variational.callbacks import CheckParametersConvergence
with model:
mean_field = pm.fit(method="advi", callbacks=[CheckParametersConvergence()])
Finished [100%]: Average Loss = 2.239
We can access inference history via .hist attribute.
plt.plot(mean_field.hist);
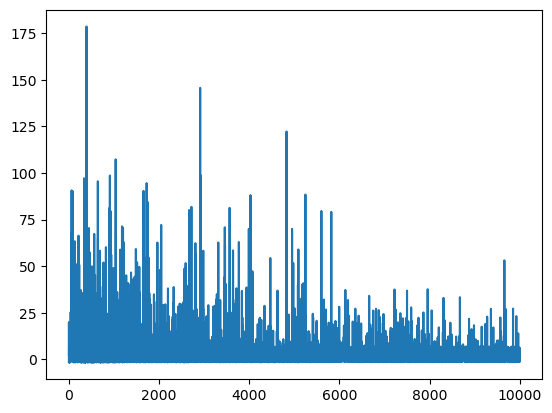
This is not a good convergence plot, despite the fact that we ran many iterations. The reason is that the mean of the ADVI approximation is close to zero, and therefore taking the relative difference (the default method) is unstable for checking convergence.
with model:
mean_field = pm.fit(
method="advi", callbacks=[pm.callbacks.CheckParametersConvergence(diff="absolute")]
)
Convergence achieved at 6200
Interrupted at 6,199 [61%]: Average Loss = 4.3808
plt.plot(mean_field.hist);
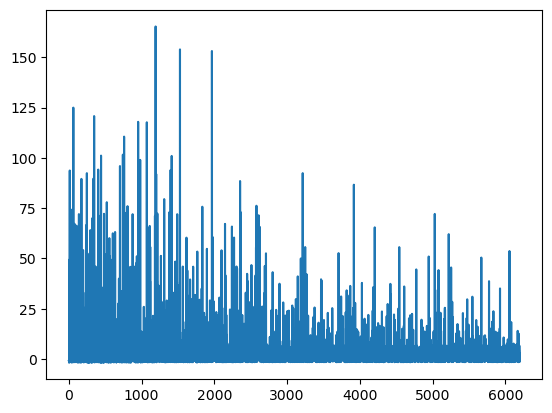
That’s much better! We’ve reached convergence after less than 5000 iterations.
Tracking parameters#
Another useful callback allows users to track parameters. It allows for the tracking of arbitrary statistics during inference, though it can be memory-hungry. Using the fit function, we do not have direct access to the approximation before inference. However, tracking parameters requires access to the approximation. We can get around this constraint by using the object-oriented (OO) API for inference.
with model:
advi = pm.ADVI()
advi.approx
<pymc.variational.approximations.MeanField at 0x7fca1daee6a0>
Different approximations have different hyperparameters. In mean-field ADVI, we have \(\rho\) and \(\mu\) (inspired by Bayes by BackProp).
advi.approx.shared_params
{'mu': mu, 'rho': rho}
There are convenient shortcuts to relevant statistics associated with the approximation. This can be useful, for example, when specifying a mass matrix for NUTS sampling:
advi.approx.mean.eval(), advi.approx.std.eval()
(array([0.34]), array([0.69314718]))
We can roll these statistics into the Tracker callback.
tracker = pm.callbacks.Tracker(
mean=advi.approx.mean.eval, # callable that returns mean
std=advi.approx.std.eval, # callable that returns std
)
Now, calling advi.fit will record the mean and standard deviation of the approximation as it runs.
approx = advi.fit(20000, callbacks=[tracker])
Finished [100%]: Average Loss = 2.2862
We can now plot both the evidence lower bound and parameter traces:
fig = plt.figure(figsize=(16, 9))
mu_ax = fig.add_subplot(221)
std_ax = fig.add_subplot(222)
hist_ax = fig.add_subplot(212)
mu_ax.plot(tracker["mean"])
mu_ax.set_title("Mean track")
std_ax.plot(tracker["std"])
std_ax.set_title("Std track")
hist_ax.plot(advi.hist)
hist_ax.set_title("Negative ELBO track");
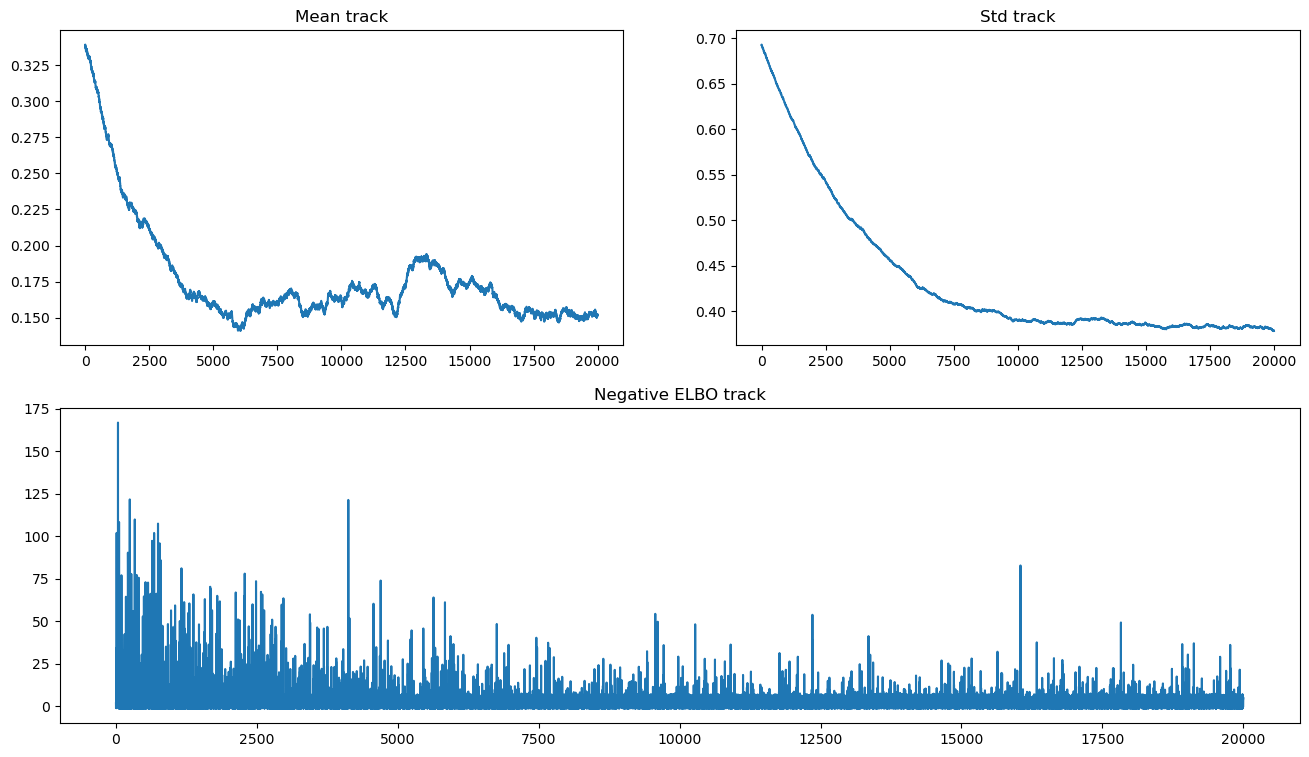
Notice that there are convergence issues with the mean, and that lack of convergence does not seem to change the ELBO trajectory significantly. As we are using the OO API, we can run the approximation longer until convergence is achieved.
advi.refine(100_000)
Finished [100%]: Average Loss = 2.1363
Let’s take a look:
fig = plt.figure(figsize=(16, 9))
mu_ax = fig.add_subplot(221)
std_ax = fig.add_subplot(222)
hist_ax = fig.add_subplot(212)
mu_ax.plot(tracker["mean"])
mu_ax.set_title("Mean track")
std_ax.plot(tracker["std"])
std_ax.set_title("Std track")
hist_ax.plot(advi.hist)
hist_ax.set_title("Negative ELBO track");
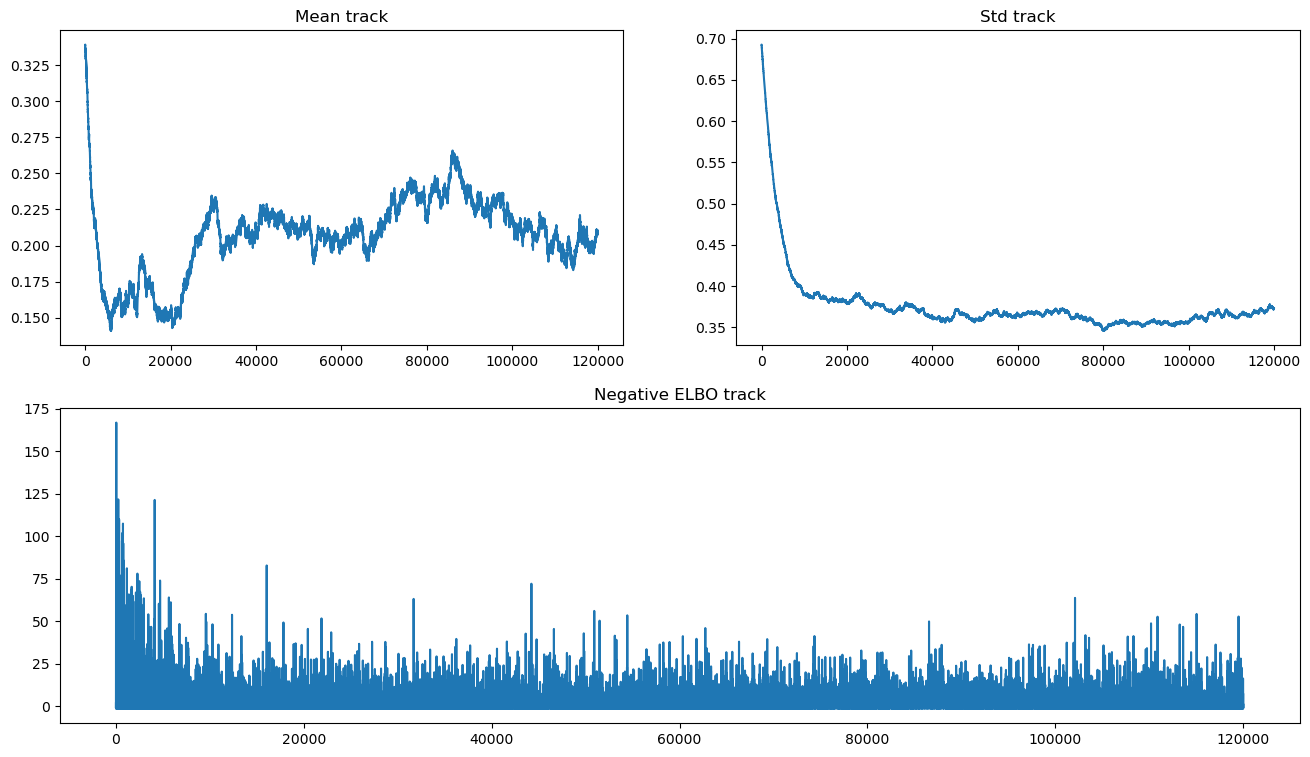
We still see evidence for lack of convergence, as the mean has devolved into a random walk. This could be the result of choosing a poor algorithm for inference. At any rate, it is unstable and can produce very different results even using different random seeds.
Let’s compare results with the NUTS output:
sns.kdeplot(trace.posterior["x"].values.flatten(), label="NUTS")
sns.kdeplot(approx.sample(20000).posterior["x"].values.flatten(), label="ADVI")
plt.legend();
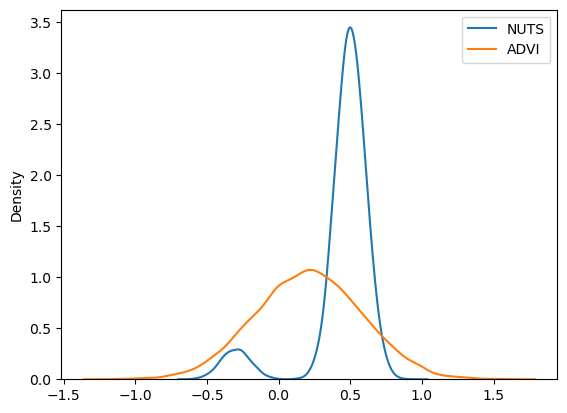
Again, we see that ADVI is not able to cope with multimodality; we can instead use SVGD, which generates an approximation based on a large number of particles.
sns.kdeplot(trace.posterior["x"].values.flatten(), label="NUTS")
sns.kdeplot(approx.sample(10000).posterior["x"].values.flatten(), label="ADVI")
sns.kdeplot(svgd_approx.sample(2000).posterior["x"].values.flatten(), label="SVGD")
plt.legend();
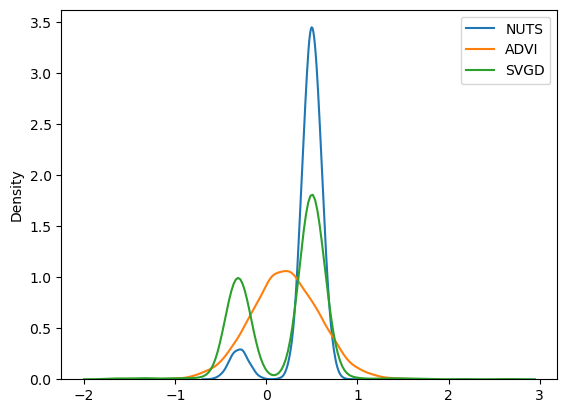
That did the trick, as we now have a multimodal approximation using SVGD.
With this, it is possible to calculate arbitrary functions of the parameters with this variational approximation. For example we can calculate \(x^2\) and \(sin(x)\), as with the NUTS model.
# recall x ~ NormalMixture
a = x**2
b = pm.math.sin(x)
To evaluate these expressions with the approximation, we need approx.sample_node.
a_sample = svgd_approx.sample_node(a)
a_sample.eval()
array(0.06251754)
a_sample.eval()
array(0.06251754)
a_sample.eval()
array(0.06251754)
Every call yields a different value from the same node. This is because it is stochastic.
By applying replacements, we are now free of the dependence on the PyMC model; instead, we now depend on the approximation. Changing it will change the distribution for stochastic nodes:
There is a more convenient way to get lots of samples at once: sample_node
a_samples = svgd_approx.sample_node(a, size=1000)
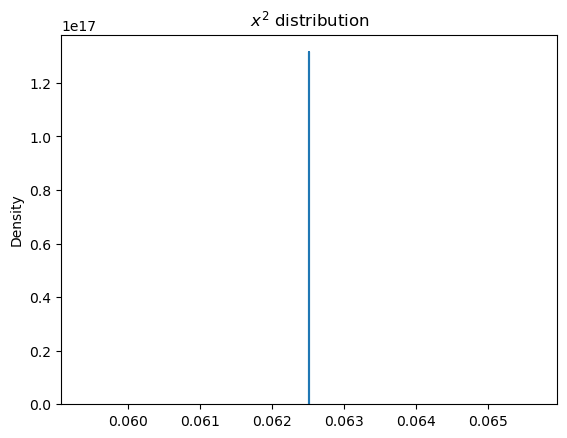
sns.kdeplot(a_samples.eval())
plt.title("$x^2$ distribution");
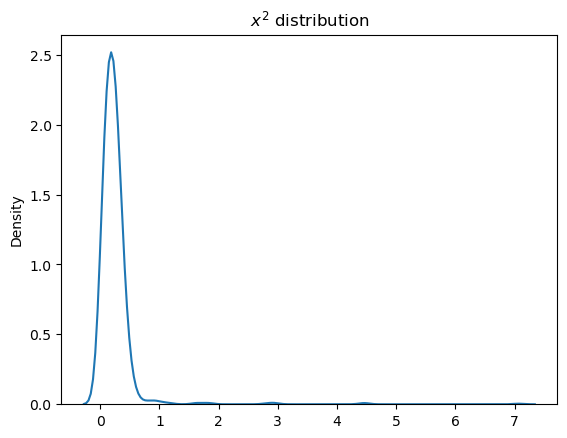
The sample_node function includes an additional dimension, so taking expectations or calculating variance is specified by axis=0.
a_samples.var(0).eval() # variance
array(0.13313996)
a_samples.mean(0).eval() # mean
array(0.24540344)
A symbolic sample size can also be specified:
import pytensor.tensor as pt
i = pt.iscalar("i")
i.tag.test_value = 1
a_samples_i = svgd_approx.sample_node(a, size=i)
a_samples_i.eval({i: 100}).shape
(100,)
a_samples_i.eval({i: 10000}).shape
(10000,)
Unfortunately the size must be a scalar value.
Multilabel logistic regression#
Let’s illustrate the use of Tracker with the famous Iris dataset. We’ll attempy multi-label classification and compute the expected accuracy score as a diagnostic.
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y)

A relatively simple model will be sufficient here because the classes are roughly linearly separable; we are going to fit multinomial logistic regression.
Xt = pytensor.shared(X_train)
yt = pytensor.shared(y_train)
with pm.Model() as iris_model:
# Coefficients for features
β = pm.Normal("β", 0, sigma=1e2, shape=(4, 3))
# Transoform to unit interval
a = pm.Normal("a", sigma=1e4, shape=(3,))
p = pt.special.softmax(Xt.dot(β) + a, axis=-1)
observed = pm.Categorical("obs", p=p, observed=yt)
Applying replacements in practice#
PyMC models have symbolic inputs for latent variables. To evaluate an expression that requires knowledge of latent variables, one needs to provide fixed values. We can use values approximated by VI for this purpose. The function sample_node removes the symbolic dependencies.
sample_node will use the whole distribution at each step, so we will use it here. We can apply more replacements in single function call using the more_replacements keyword argument in both replacement functions.
HINT: You can use
more_replacementsargument when callingfittoo:
pm.fit(more_replacements={full_data: minibatch_data})
inference.fit(more_replacements={full_data: minibatch_data})
with iris_model:
# We'll use SVGD
inference = pm.SVGD(n_particles=500, jitter=1)
# Local reference to approximation
approx = inference.approx
# Here we need `more_replacements` to change train_set to test_set
test_probs = approx.sample_node(p, more_replacements={Xt: X_test}, size=100)
# For train set no more replacements needed
train_probs = approx.sample_node(p)
By applying the code above, we now have 100 sampled probabilities (default number for sample_node is None) for each observation.
Next we create symbolic expressions for sampled accuracy scores:
Tracker expects callables so we can pass .eval method of PyTensor node that is function itself.
Calls to this function are cached so they can be reused.
eval_tracker = pm.callbacks.Tracker(
test_accuracy=test_accuracy.eval, train_accuracy=train_accuracy.eval
)
inference.fit(100, callbacks=[eval_tracker]);
_, ax = plt.subplots(1, 1)
df = pd.DataFrame(eval_tracker["test_accuracy"]).T.melt()
sns.lineplot(x="variable", y="value", data=df, color="red", ax=ax)
ax.plot(eval_tracker["train_accuracy"], color="blue")
ax.set_xlabel("epoch")
plt.legend(["test_accuracy", "train_accuracy"])
plt.title("Training Progress");
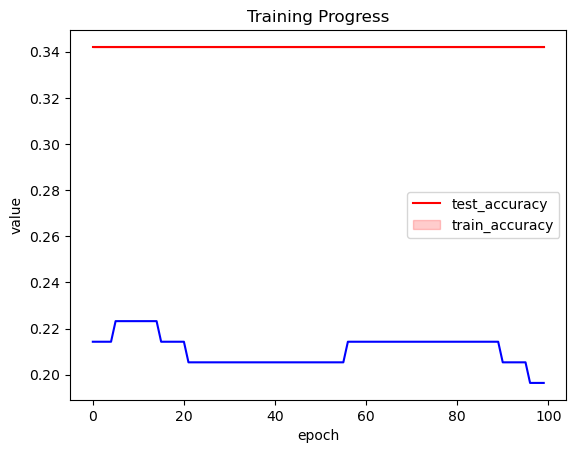
Training does not seem to be working here. Let’s use a different optimizer and boost the learning rate.
inference.fit(400, obj_optimizer=pm.adamax(learning_rate=0.1), callbacks=[eval_tracker]);
_, ax = plt.subplots(1, 1)
df = pd.DataFrame(np.asarray(eval_tracker["test_accuracy"])).T.melt()
sns.lineplot(x="variable", y="value", data=df, color="red", ax=ax)
ax.plot(eval_tracker["train_accuracy"], color="blue")
ax.set_xlabel("epoch")
plt.legend(["test_accuracy", "train_accuracy"])
plt.title("Training Progress");
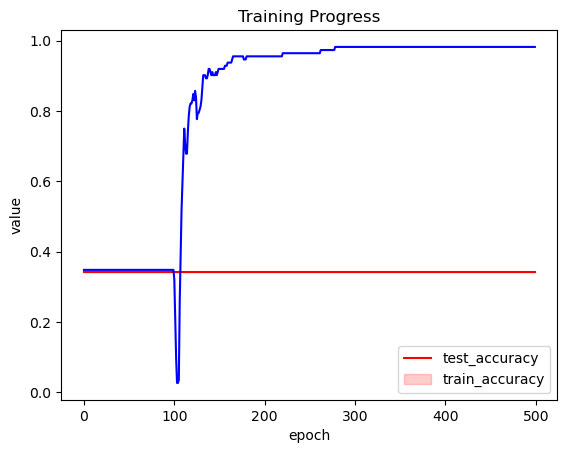
This is much better!
So, Tracker allows us to monitor our approximation and choose good training schedule.
Minibatches#
When dealing with large datasets, using minibatch training can drastically speed up and improve approximation performance. Large datasets impose a hefty cost on the computation of gradients.
There is a nice API in PyMC to handle these cases, which is available through the pm.Minibatch class. The minibatch is just a highly specialized PyTensor tensor.
To demonstrate, let’s simulate a large quantity of data:
# Raw values
data = np.random.rand(40000, 100)
# Scaled values
data *= np.random.randint(1, 10, size=(100,))
# Shifted values
data += np.random.rand(100) * 10
For comparison, let’s fit a model without minibatch processing:
with pm.Model() as model:
mu = pm.Flat("mu", shape=(100,))
sd = pm.HalfNormal("sd", shape=(100,))
lik = pm.Normal("lik", mu, sigma=sd, observed=data)
Just for fun, let’s create a custom special purpose callback to halt slow optimization. Here we define a callback that causes a hard stop when approximation runs too slowly:
def stop_after_10(approx, loss_history, i):
if (i > 0) and (i % 10) == 0:
raise StopIteration("I was slow, sorry")
with model:
advifit = pm.fit(callbacks=[stop_after_10])
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Cell In[66], line 2
1 with model:
----> 2 advifit = pm.fit(callbacks=[stop_after_10])
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/variational/inference.py:747, in fit(n, method, model, random_seed, start, start_sigma, inf_kwargs, **kwargs)
745 else:
746 raise TypeError(f"method should be one of {set(_select.keys())} or Inference instance")
--> 747 return inference.fit(n, **kwargs)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/variational/inference.py:138, in Inference.fit(self, n, score, callbacks, progressbar, **kwargs)
136 callbacks = []
137 score = self._maybe_score(score)
--> 138 step_func = self.objective.step_function(score=score, **kwargs)
139 if progressbar:
140 progress = progress_bar(range(n), display=progressbar)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/configparser.py:47, in _ChangeFlagsDecorator.__call__.<locals>.res(*args, **kwargs)
44 @wraps(f)
45 def res(*args, **kwargs):
46 with self:
---> 47 return f(*args, **kwargs)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/variational/opvi.py:387, in ObjectiveFunction.step_function(self, obj_n_mc, tf_n_mc, obj_optimizer, test_optimizer, more_obj_params, more_tf_params, more_updates, more_replacements, total_grad_norm_constraint, score, fn_kwargs)
385 seed = self.approx.rng.randint(2**30, dtype=np.int64)
386 if score:
--> 387 step_fn = compile_pymc([], updates.loss, updates=updates, random_seed=seed, **fn_kwargs)
388 else:
389 step_fn = compile_pymc([], [], updates=updates, random_seed=seed, **fn_kwargs)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/pytensorf.py:1121, in compile_pymc(inputs, outputs, random_seed, mode, **kwargs)
1119 opt_qry = mode.provided_optimizer.including("random_make_inplace", check_parameter_opt)
1120 mode = Mode(linker=mode.linker, optimizer=opt_qry)
-> 1121 pytensor_function = pytensor.function(
1122 inputs,
1123 outputs,
1124 updates={**rng_updates, **kwargs.pop("updates", {})},
1125 mode=mode,
1126 **kwargs,
1127 )
1128 return pytensor_function
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/compile/function/__init__.py:315, in function(inputs, outputs, mode, updates, givens, no_default_updates, accept_inplace, name, rebuild_strict, allow_input_downcast, profile, on_unused_input)
309 fn = orig_function(
310 inputs, outputs, mode=mode, accept_inplace=accept_inplace, name=name
311 )
312 else:
313 # note: pfunc will also call orig_function -- orig_function is
314 # a choke point that all compilation must pass through
--> 315 fn = pfunc(
316 params=inputs,
317 outputs=outputs,
318 mode=mode,
319 updates=updates,
320 givens=givens,
321 no_default_updates=no_default_updates,
322 accept_inplace=accept_inplace,
323 name=name,
324 rebuild_strict=rebuild_strict,
325 allow_input_downcast=allow_input_downcast,
326 on_unused_input=on_unused_input,
327 profile=profile,
328 output_keys=output_keys,
329 )
330 return fn
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/compile/function/pfunc.py:367, in pfunc(params, outputs, mode, updates, givens, no_default_updates, accept_inplace, name, rebuild_strict, allow_input_downcast, profile, on_unused_input, output_keys, fgraph)
353 profile = ProfileStats(message=profile)
355 inputs, cloned_outputs = construct_pfunc_ins_and_outs(
356 params,
357 outputs,
(...)
364 fgraph=fgraph,
365 )
--> 367 return orig_function(
368 inputs,
369 cloned_outputs,
370 mode,
371 accept_inplace=accept_inplace,
372 name=name,
373 profile=profile,
374 on_unused_input=on_unused_input,
375 output_keys=output_keys,
376 fgraph=fgraph,
377 )
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/compile/function/types.py:1766, in orig_function(inputs, outputs, mode, accept_inplace, name, profile, on_unused_input, output_keys, fgraph)
1754 m = Maker(
1755 inputs,
1756 outputs,
(...)
1763 fgraph=fgraph,
1764 )
1765 with config.change_flags(compute_test_value="off"):
-> 1766 fn = m.create(defaults)
1767 finally:
1768 t2 = time.perf_counter()
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/compile/function/types.py:1659, in FunctionMaker.create(self, input_storage, trustme, storage_map)
1656 start_import_time = pytensor.link.c.cmodule.import_time
1658 with config.change_flags(traceback__limit=config.traceback__compile_limit):
-> 1659 _fn, _i, _o = self.linker.make_thunk(
1660 input_storage=input_storage_lists, storage_map=storage_map
1661 )
1663 end_linker = time.perf_counter()
1665 linker_time = end_linker - start_linker
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/basic.py:254, in LocalLinker.make_thunk(self, input_storage, output_storage, storage_map, **kwargs)
247 def make_thunk(
248 self,
249 input_storage: Optional["InputStorageType"] = None,
(...)
252 **kwargs,
253 ) -> Tuple["BasicThunkType", "InputStorageType", "OutputStorageType"]:
--> 254 return self.make_all(
255 input_storage=input_storage,
256 output_storage=output_storage,
257 storage_map=storage_map,
258 )[:3]
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/vm.py:1246, in VMLinker.make_all(self, profiler, input_storage, output_storage, storage_map)
1241 thunk_start = time.perf_counter()
1242 # no-recycling is done at each VM.__call__ So there is
1243 # no need to cause duplicate c code by passing
1244 # no_recycling here.
1245 thunks.append(
-> 1246 node.op.make_thunk(node, storage_map, compute_map, [], impl=impl)
1247 )
1248 linker_make_thunk_time[node] = time.perf_counter() - thunk_start
1249 if not hasattr(thunks[-1], "lazy"):
1250 # We don't want all ops maker to think about lazy Ops.
1251 # So if they didn't specify that its lazy or not, it isn't.
1252 # If this member isn't present, it will crash later.
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/op.py:131, in COp.make_thunk(self, node, storage_map, compute_map, no_recycling, impl)
127 self.prepare_node(
128 node, storage_map=storage_map, compute_map=compute_map, impl="c"
129 )
130 try:
--> 131 return self.make_c_thunk(node, storage_map, compute_map, no_recycling)
132 except (NotImplementedError, MethodNotDefined):
133 # We requested the c code, so don't catch the error.
134 if impl == "c":
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/op.py:96, in COp.make_c_thunk(self, node, storage_map, compute_map, no_recycling)
94 print(f"Disabling C code for {self} due to unsupported float16")
95 raise NotImplementedError("float16")
---> 96 outputs = cl.make_thunk(
97 input_storage=node_input_storage, output_storage=node_output_storage
98 )
99 thunk, node_input_filters, node_output_filters = outputs
101 @is_cthunk_wrapper_type
102 def rval():
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/basic.py:1202, in CLinker.make_thunk(self, input_storage, output_storage, storage_map, cache, **kwargs)
1167 """Compile this linker's `self.fgraph` and return a function that performs the computations.
1168
1169 The return values can be used as follows:
(...)
1199
1200 """
1201 init_tasks, tasks = self.get_init_tasks()
-> 1202 cthunk, module, in_storage, out_storage, error_storage = self.__compile__(
1203 input_storage, output_storage, storage_map, cache
1204 )
1206 res = _CThunk(cthunk, init_tasks, tasks, error_storage, module)
1207 res.nodes = self.node_order
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/basic.py:1122, in CLinker.__compile__(self, input_storage, output_storage, storage_map, cache)
1120 input_storage = tuple(input_storage)
1121 output_storage = tuple(output_storage)
-> 1122 thunk, module = self.cthunk_factory(
1123 error_storage,
1124 input_storage,
1125 output_storage,
1126 storage_map,
1127 cache,
1128 )
1129 return (
1130 thunk,
1131 module,
(...)
1140 error_storage,
1141 )
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/basic.py:1647, in CLinker.cthunk_factory(self, error_storage, in_storage, out_storage, storage_map, cache)
1645 if cache is None:
1646 cache = get_module_cache()
-> 1647 module = cache.module_from_key(key=key, lnk=self)
1649 vars = self.inputs + self.outputs + self.orphans
1650 # List of indices that should be ignored when passing the arguments
1651 # (basically, everything that the previous call to uniq eliminated)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/cmodule.py:1231, in ModuleCache.module_from_key(self, key, lnk)
1229 try:
1230 location = dlimport_workdir(self.dirname)
-> 1231 module = lnk.compile_cmodule(location)
1232 name = module.__file__
1233 assert name.startswith(location)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/basic.py:1546, in CLinker.compile_cmodule(self, location)
1544 try:
1545 _logger.debug(f"LOCATION {location}")
-> 1546 module = c_compiler.compile_str(
1547 module_name=mod.code_hash,
1548 src_code=src_code,
1549 location=location,
1550 include_dirs=self.header_dirs(),
1551 lib_dirs=self.lib_dirs(),
1552 libs=libs,
1553 preargs=preargs,
1554 )
1555 except Exception as e:
1556 e.args += (str(self.fgraph),)
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/link/c/cmodule.py:2591, in GCC_compiler.compile_str(module_name, src_code, location, include_dirs, lib_dirs, libs, preargs, py_module, hide_symbols)
2588 print(" ".join(cmd), file=sys.stderr)
2590 try:
-> 2591 p_out = output_subprocess_Popen(cmd)
2592 compile_stderr = p_out[1].decode()
2593 except Exception:
2594 # An exception can occur e.g. if `g++` is not found.
File ~/mambaforge/envs/pie/lib/python3.9/site-packages/pytensor/utils.py:261, in output_subprocess_Popen(command, **params)
258 p = subprocess_Popen(command, **params)
259 # we need to use communicate to make sure we don't deadlock around
260 # the stdout/stderr pipe.
--> 261 out = p.communicate()
262 return out + (p.returncode,)
File ~/mambaforge/envs/pie/lib/python3.9/subprocess.py:1130, in Popen.communicate(self, input, timeout)
1127 endtime = None
1129 try:
-> 1130 stdout, stderr = self._communicate(input, endtime, timeout)
1131 except KeyboardInterrupt:
1132 # https://bugs.python.org/issue25942
1133 # See the detailed comment in .wait().
1134 if timeout is not None:
File ~/mambaforge/envs/pie/lib/python3.9/subprocess.py:1977, in Popen._communicate(self, input, endtime, orig_timeout)
1970 self._check_timeout(endtime, orig_timeout,
1971 stdout, stderr,
1972 skip_check_and_raise=True)
1973 raise RuntimeError( # Impossible :)
1974 '_check_timeout(..., skip_check_and_raise=True) '
1975 'failed to raise TimeoutExpired.')
-> 1977 ready = selector.select(timeout)
1978 self._check_timeout(endtime, orig_timeout, stdout, stderr)
1980 # XXX Rewrite these to use non-blocking I/O on the file
1981 # objects; they are no longer using C stdio!
File ~/mambaforge/envs/pie/lib/python3.9/selectors.py:416, in _PollLikeSelector.select(self, timeout)
414 ready = []
415 try:
--> 416 fd_event_list = self._selector.poll(timeout)
417 except InterruptedError:
418 return ready
KeyboardInterrupt:
Inference is too slow, taking several seconds per iteration; fitting the approximation would have taken hours!
Now let’s use minibatches. At every iteration, we will draw 500 random values:
Remember to set
total_sizein observed
total_size is an important parameter that allows PyMC to infer the right way of rescaling densities. If it is not set, you are likely to get completely wrong results. For more information please refer to the comprehensive documentation of pm.Minibatch.
X = pm.Minibatch(data, batch_size=500)
with pm.Model() as model:
mu = pm.Normal("mu", 0, sigma=1e5, shape=(100,))
sd = pm.HalfNormal("sd", shape=(100,))
likelihood = pm.Normal("likelihood", mu, sigma=sd, observed=X, total_size=data.shape)
with model:
advifit = pm.fit()
Finished [100%]: Average Loss = 1.5101e+05
plt.plot(advifit.hist);
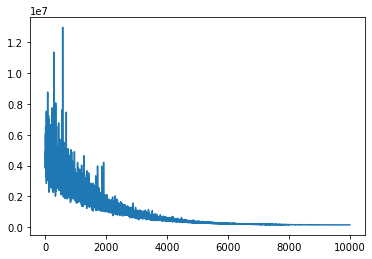
Minibatch inference is dramatically faster. Multidimensional minibatches may be needed for some corner cases where you do matrix factorization or model is very wide.
Here is the docstring for Minibatch to illustrate how it can be customized.
print(pm.Minibatch.__doc__)
Multidimensional minibatch that is pure TensorVariable
Parameters
----------
data: np.ndarray
initial data
batch_size: ``int`` or ``List[int|tuple(size, random_seed)]``
batch size for inference, random seed is needed
for child random generators
dtype: ``str``
cast data to specific type
broadcastable: tuple[bool]
change broadcastable pattern that defaults to ``(False, ) * ndim``
name: ``str``
name for tensor, defaults to "Minibatch"
random_seed: ``int``
random seed that is used by default
update_shared_f: ``callable``
returns :class:`ndarray` that will be carefully
stored to underlying shared variable
you can use it to change source of
minibatches programmatically
in_memory_size: ``int`` or ``List[int|slice|Ellipsis]``
data size for storing in ``aesara.shared``
Attributes
----------
shared: shared tensor
Used for storing data
minibatch: minibatch tensor
Used for training
Notes
-----
Below is a common use case of Minibatch with variational inference.
Importantly, we need to make PyMC "aware" that a minibatch is being used in inference.
Otherwise, we will get the wrong :math:`logp` for the model.
the density of the model ``logp`` that is affected by Minibatch. See more in the examples below.
To do so, we need to pass the ``total_size`` parameter to the observed node, which correctly scales
the density of the model ``logp`` that is affected by Minibatch. See more in the examples below.
Examples
--------
Consider we have `data` as follows:
>>> data = np.random.rand(100, 100)
if we want a 1d slice of size 10 we do
>>> x = Minibatch(data, batch_size=10)
Note that your data is cast to ``floatX`` if it is not integer type
But you still can add the ``dtype`` kwarg for :class:`Minibatch`
if you need more control.
If we want 10 sampled rows and columns
``[(size, seed), (size, seed)]`` we can use
>>> x = Minibatch(data, batch_size=[(10, 42), (10, 42)], dtype='int32')
>>> assert str(x.dtype) == 'int32'
Or, more simply, we can use the default random seed = 42
``[size, size]``
>>> x = Minibatch(data, batch_size=[10, 10])
In the above, `x` is a regular :class:`TensorVariable` that supports any math operations:
>>> assert x.eval().shape == (10, 10)
You can pass the Minibatch `x` to your desired model:
>>> with pm.Model() as model:
... mu = pm.Flat('mu')
... sigma = pm.HalfNormal('sigma')
... lik = pm.Normal('lik', mu, sigma, observed=x, total_size=(100, 100))
Then you can perform regular Variational Inference out of the box
>>> with model:
... approx = pm.fit()
Important note: :class:``Minibatch`` has ``shared``, and ``minibatch`` attributes
you can call later:
>>> x.set_value(np.random.laplace(size=(100, 100)))
and minibatches will be then from new storage
it directly affects ``x.shared``.
A less convenient convenient, but more explicit, way to achieve the same
thing:
>>> x.shared.set_value(pm.floatX(np.random.laplace(size=(100, 100))))
The programmatic way to change storage is as follows
I import ``partial`` for simplicity
>>> from functools import partial
>>> datagen = partial(np.random.laplace, size=(100, 100))
>>> x = Minibatch(datagen(), batch_size=10, update_shared_f=datagen)
>>> x.update_shared()
To be more concrete about how we create a minibatch, here is a demo:
1. create a shared variable
>>> shared = aesara.shared(data)
2. take a random slice of size 10:
>>> ridx = pm.at_rng().uniform(size=(10,), low=0, high=data.shape[0]-1e-10).astype('int64')
3) take the resulting slice:
>>> minibatch = shared[ridx]
That's done. Now you can use this minibatch somewhere else.
You can see that the implementation does not require a fixed shape
for the shared variable. Feel free to use that if needed.
*FIXME: What is "that" which we can use here? A fixed shape? Should this say
"but feel free to put a fixed shape on the shared variable, if appropriate?"*
Suppose you need to make some replacements in the graph, e.g. change the minibatch to testdata
>>> node = x ** 2 # arbitrary expressions on minibatch `x`
>>> testdata = pm.floatX(np.random.laplace(size=(1000, 10)))
Then you should create a `dict` with replacements:
>>> replacements = {x: testdata}
>>> rnode = aesara.clone_replace(node, replacements)
>>> assert (testdata ** 2 == rnode.eval()).all()
*FIXME: In the following, what is the **reason** to replace the Minibatch variable with
its shared variable? And in the following, the `rnode` is a **new** node, not a modification
of a previously existing node, correct?*
To replace a minibatch with its shared variable you should do
the same things. The Minibatch variable is accessible through the `minibatch` attribute.
For example
>>> replacements = {x.minibatch: x.shared}
>>> rnode = aesara.clone_replace(node, replacements)
For more complex slices some more code is needed that can seem not so clear
>>> moredata = np.random.rand(10, 20, 30, 40, 50)
The default ``total_size`` that can be passed to PyMC random node
is then ``(10, 20, 30, 40, 50)`` but can be less verbose in some cases
1. Advanced indexing, ``total_size = (10, Ellipsis, 50)``
>>> x = Minibatch(moredata, [2, Ellipsis, 10])
We take the slice only for the first and last dimension
>>> assert x.eval().shape == (2, 20, 30, 40, 10)
2. Skipping a particular dimension, ``total_size = (10, None, 30)``:
>>> x = Minibatch(moredata, [2, None, 20])
>>> assert x.eval().shape == (2, 20, 20, 40, 50)
3. Mixing both of these together, ``total_size = (10, None, 30, Ellipsis, 50)``:
>>> x = Minibatch(moredata, [2, None, 20, Ellipsis, 10])
>>> assert x.eval().shape == (2, 20, 20, 40, 10)
Watermark#
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Sun Nov 20 2022
Python implementation: CPython
Python version : 3.10.4
IPython version : 8.4.0
sys : 3.10.4 | packaged by conda-forge | (main, Mar 24 2022, 17:39:37) [Clang 12.0.1 ]
pymc : 4.3.0
seaborn : 0.11.2
arviz : 0.13.0
numpy : 1.22.4
matplotlib: 3.5.2
aesara : 2.8.9+11.ge8eed6c18
pandas : 1.4.2
Watermark: 2.3.1
License notice#
All the notebooks in this example gallery are provided under the MIT License which allows modification, and redistribution for any use provided the copyright and license notices are preserved.
Citing PyMC examples#
To cite this notebook, use the DOI provided by Zenodo for the pymc-examples repository.
Important
Many notebooks are adapted from other sources: blogs, books… In such cases you should cite the original source as well.
Also remember to cite the relevant libraries used by your code.
Here is an citation template in bibtex:
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
which once rendered could look like: