View On GitHub Open In Binder Open In Colab

Discrete Choice and Random Utility Models#

Attention

This notebook uses libraries that are not PyMC dependencies and therefore need to be installed specifically to run this notebook. Open the dropdown below for extra guidance.

Extra dependencies install instructions

In order to run this notebook (either locally or on binder) you won’t only need a working PyMC installation with all optional dependencies, but also to install some extra dependencies. For advise on installing PyMC itself, please refer to Installation

You can install these dependencies with your preferred package manager, we provide as an example the pip and conda commands below.

$ pip install jax, jaxlib, numpyro

Note that if you want (or need) to install the packages from inside the notebook instead of the command line, you can install the packages by running a variation of the pip command:

import sys

!{sys.executable} -m pip install jax, jaxlib, numpyro

You should not run !pip install as it might install the package in a different environment and not be available from the Jupyter notebook even if installed.

Another alternative is using conda instead:

$ conda install jax, jaxlib, numpyro

when installing scientific python packages with conda, we recommend using conda forge

import arviz as az
import numpy as np  # For vectorized math operations
import pandas as pd  # For file input/output
import pymc as pm
import pytensor.tensor as pt

from matplotlib import pyplot as plt
from matplotlib.lines import Line2D

%config InlineBackend.figure_format = 'retina'  # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)

Discrete Choice Modelling: The Idea#

Discrete choice modelling is related to the idea of a latent utility scale as discussed in Regression Models with Ordered Categorical Outcomes, but it generalises the idea to decision making. It posits that human decision making can be modelled as a function of latent/subjective utility measurements over a set of mutually exclusive alternatives. The theory states that any decision maker will go with the option that maximises their subjective utility, and that utility can be modelled as a latent linear function of observable features of the world.

The idea is perhaps most famously applied by Daniel McFadden in the 1970s to predict the market share accruing to transportation choices (i.e. car, rail, walking etc..) in California after the proposed introduction of BART light rail system. It’s worth pausing on that point. The theory is one of micro level human decision making that has, in real applications, been scaled up to make broadly accurate macro level predictions. For more details we recommend Train [2009]

We don’t need to be too credulous either. This is merely a statistical model and success here is entirely dependent on the skill of modeller and the available measurements coupled with plausible theory. But it’s worth noting the scale of the ambition underlying these models. The structure of the model encourages you to articulate your theory of the decision makers and the environment they inhabit.

The Data#

In this example, we’ll examine the technique of discrete choice modelling using a (i) heating system data set from the R mlogit package and (ii) repeat choice data set over cracker brands. We’ll be pursuing a Bayesian approach to estimating the models rather than the MLE methodology reported in their vigenette. The first data set shows household choices over offers of heating systems in California. The observations consist of single-family houses in California that were newly built and had central air-conditioning. Five types of systems are considered to have been possible:

  • gas central (gc),

  • gas room (gr),

  • electric central (ec),

  • electric room (er),

  • heat pump (hp).

The data set reports the installation ic.alt and operating costs oc.alt each household was faced with for each of the five alternatives with some broad demographic information about the household and crucially the choice depvar. This is what one choice scenario over the five alternative looks like in the data:

try:
    wide_heating_df = pd.read_csv("../data/heating_data_r.csv")
except:
    wide_heating_df = pd.read_csv(pm.get_data("heating_data_r.csv"))

wide_heating_df[wide_heating_df["idcase"] == 1]
idcase depvar ic.gc ic.gr ic.ec ic.er ic.hp oc.gc oc.gr oc.ec oc.er oc.hp income agehed rooms region
0 1 gc 866.0 962.64 859.9 995.76 1135.5 199.69 151.72 553.34 505.6 237.88 7 25 6 ncostl

The core idea of these kinds of models is to conceive of this scenario as a choice over exhaustive options with attached latent utility. The utility ascribed to each option is viewed as a linear combination of the attributes for each option. The utility ascribed to each alternative drives the probability of choosing amongst each option. For each \(j\) in all the alternatives \(Alt = \{ gc, gr, ec, er, hp \}\) which is assumed to take a Gumbel distribution because this has a particularly nice mathematical property.

\[ \mathbf{U} \sim Gumbel \]
\[\begin{split} \begin{pmatrix} u_{gc} \\ u_{gr} \\ u_{ec} \\ u_{er} \\ u_{hp} \\ \end{pmatrix} = \begin{pmatrix} gc_{ic} & gc_{oc} \\ gr_{ic} & gr_{oc} \\ ec_{ic} & ec_{oc} \\ er_{ic} & er_{oc} \\ hp_{ic} & hp_{oc} \\ \end{pmatrix} \begin{pmatrix} \beta_{ic} \\ \beta_{oc} \\ \end{pmatrix} \end{split}\]

This assumption proves to be mathematically convenient because the difference between two Gumbel distributions can be modelled as a logistic function, meaning we can model a contrast difference among multiple alternatives with the softmax function. Details of the derivation can be found in Train [2009]

\[ \text{softmax}(u)_{j} = \frac{\exp(u_{j})}{\sum_{q=1}^{J}\exp(u_{q})} \]

The model then assumes that decision maker chooses the option that maximises their subjective utility. The individual utility functions can be richly parameterised. The model is identified just when the utility measures of the alternatives are benchmarked against the fixed utility of the “outside good.” The last quantity is often fixed at 0 to aid parameter identification on alternative-specific parameters as we’ll see below.

\[\begin{split}\begin{pmatrix} u_{gc} \\ u_{gr} \\ u_{ec} \\ u_{er} \\ 0 \\ \end{pmatrix} \end{split}\]

With all these constraints applied we can build out conditional random utility model and it’s hierarchical variants. Like nearly all subjects in statistics the precise vocabulary for the model specification is overloaded. The conditional logit parameters \(\beta\) may be fixed at the level of the individual, but can vary across individuals and the alternatives gc, gr, ec, er too. In this manner we can compose an elaborate theory of how we expect drivers of subjective utility to change the market share amongst a set of competing goods.

Digression on Data Formats#

Discrete choice models are often estimated using a long-data format where each choice scenario is represented with a row per alternative ID and a binary flag denoting the chosen option in each scenario. This data format is recommended for estimating these kinds of models in stan and in pylogit. The reason for doing this is that once the columns installation_costs and operating_costs have been pivoted in this fashion it’s easier to include them in matrix calculations.

try:
    long_heating_df = pd.read_csv("../data/long_heating_data.csv")
except:
    long_heating_df = pd.read_csv(pm.get_data("long_heating_data.csv"))

columns = [c for c in long_heating_df.columns if c != "Unnamed: 0"]
long_heating_df[long_heating_df["idcase"] == 1][columns]
idcase alt_id choice depvar income agehed rooms region installation_costs operating_costs
0 1 1 1 gc 7 25 6 ncostl 866.00 199.69
1 1 2 0 gc 7 25 6 ncostl 962.64 151.72
2 1 3 0 gc 7 25 6 ncostl 859.90 553.34
3 1 4 0 gc 7 25 6 ncostl 995.76 505.60
4 1 5 0 gc 7 25 6 ncostl 1135.50 237.88

The Basic Model#

We will show here how to incorporate the utility specifications in PyMC. PyMC is a nice interface for this kind of modelling because it can express the model quite cleanly following the natural mathematical expression for this system of equations. You can see in this simple model how we go about constructing equations for the utility measure of each alternative seperately, and then stacking them together to create the input matrix for our softmax transform.

N = wide_heating_df.shape[0]
observed = pd.Categorical(wide_heating_df["depvar"]).codes
coords = {
    "alts_probs": ["ec", "er", "gc", "gr", "hp"],
    "obs": range(N),
}

with pm.Model(coords=coords) as model_1:
    beta_ic = pm.Normal("beta_ic", 0, 1)
    beta_oc = pm.Normal("beta_oc", 0, 1)

    ## Construct Utility matrix and Pivot
    u0 = beta_ic * wide_heating_df["ic.ec"] + beta_oc * wide_heating_df["oc.ec"]
    u1 = beta_ic * wide_heating_df["ic.er"] + beta_oc * wide_heating_df["oc.er"]
    u2 = beta_ic * wide_heating_df["ic.gc"] + beta_oc * wide_heating_df["oc.gc"]
    u3 = beta_ic * wide_heating_df["ic.gr"] + beta_oc * wide_heating_df["oc.gr"]
    u4 = beta_ic * wide_heating_df["ic.hp"] + beta_oc * wide_heating_df["oc.hp"]
    s = pm.math.stack([u0, u1, u2, u3, u4]).T

    ## Apply Softmax Transform
    p_ = pm.Deterministic("p", pm.math.softmax(s, axis=1), dims=("obs", "alts_probs"))

    ## Likelihood
    choice_obs = pm.Categorical("y_cat", p=p_, observed=observed, dims="obs")

    idata_m1 = pm.sample_prior_predictive()
    idata_m1.extend(
        pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}, random_seed=101)
    )
    idata_m1.extend(pm.sample_posterior_predictive(idata_m1))

pm.model_to_graphviz(model_1)

Sampling: [beta_ic, beta_oc, y_cat]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
  warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)

Compiling...
Compilation time =  0:00:01.195286
Sampling...

Sampling time =  0:00:02.097556
Transforming variables...
Transformation time =  0:00:00.396818
Computing Log Likelihood...

Sampling: [y_cat]

Log Likelihood time =  0:00:00.638968
100.00% [4000/4000 00:06<00:00]
../_images/5682d6772279c2b0b3a24de69219c940e2df544fb98cd92b9ccedf7ace484026.svg

Note that you need to be careful with the encoding of the outcome variable. The categorical ordering should reflect the ordering of the utilities as they are stacked into the softmax transform and then fed into the likelihood term.

idata_m1
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:     (chain: 4, draw: 1000, obs: 900, alts_probs: 5)
Coordinates:
  * chain       (chain) int64 0 1 2 3
  * draw        (draw) int64 0 1 2 3 4 5 6 7 ... 992 993 994 995 996 997 998 999
  * obs         (obs) int64 0 1 2 3 4 5 6 7 ... 892 893 894 895 896 897 898 899
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
Data variables:
    beta_ic     (chain, draw) float64 -0.006063 -0.006218 ... -0.005608
    beta_oc     (chain, draw) float64 -0.004401 -0.00453 ... -0.004273 -0.004929
    p           (chain, draw, obs, alts_probs) float64 0.09993 ... 0.02927
Attributes:
    created_at:     2025-03-22T20:10:25.635782
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:  (chain: 4, draw: 1000, obs: 900)
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999
  * obs      (obs) int64 0 1 2 3 4 5 6 7 8 ... 892 893 894 895 896 897 898 899
Data variables:
    y_cat    (chain, draw, obs) int64 4 2 3 2 0 0 2 3 4 2 ... 2 2 2 3 3 4 2 0 2
Attributes:
    created_at:                 2025-03-22T20:10:32.518585
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:      (chain: 4, draw: 1000, y_cat_dim_0: 1, y_cat_dim_1: 900)
Coordinates:
  * chain        (chain) int64 0 1 2 3
  * draw         (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
  * y_cat_dim_0  (y_cat_dim_0) int64 0
  * y_cat_dim_1  (y_cat_dim_1) int64 0 1 2 3 4 5 6 ... 894 895 896 897 898 899
Data variables:
    y_cat        (chain, draw, y_cat_dim_0, y_cat_dim_1) float64 -0.7837 ... ...
Attributes:
    created_at:     2025-03-22T20:10:25.639865
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:          (chain: 4, draw: 1000)
Coordinates:
  * chain            (chain) int64 0 1 2 3
  * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
Data variables:
    acceptance_rate  (chain, draw) float64 0.9776 1.0 0.9124 ... 0.7535 0.9359
    step_size        (chain, draw) float64 0.08947 0.08947 ... 0.09166 0.09166
    diverging        (chain, draw) bool False False False ... False False False
    energy           (chain, draw) float64 1.098e+03 1.097e+03 ... 1.099e+03
    n_steps          (chain, draw) int64 3 3 3 3 3 3 3 3 3 ... 3 3 3 3 3 3 3 3 3
    tree_depth       (chain, draw) int64 2 2 2 2 2 2 2 2 2 ... 2 2 2 2 2 2 2 2 2
    lp               (chain, draw) float64 1.097e+03 1.097e+03 ... 1.099e+03
Attributes:
    created_at:     2025-03-22T20:10:25.638552
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:     (chain: 1, draw: 500, obs: 900, alts_probs: 5)
Coordinates:
  * chain       (chain) int64 0
  * draw        (draw) int64 0 1 2 3 4 5 6 7 ... 492 493 494 495 496 497 498 499
  * obs         (obs) int64 0 1 2 3 4 5 6 7 ... 892 893 894 895 896 897 898 899
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
Data variables:
    beta_oc     (chain, draw) float64 0.3508 0.4991 0.04808 ... -0.3669 -0.2846
    beta_ic     (chain, draw) float64 1.281 -0.1326 0.78 ... 1.392 1.543 0.09659
    p           (chain, draw, obs, alts_probs) float64 6.131e-106 ... 0.9994
Attributes:
    created_at:                 2025-03-22T20:10:20.506855
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:  (chain: 1, draw: 500, obs: 900)
Coordinates:
  * chain    (chain) int64 0
  * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 492 493 494 495 496 497 498 499
  * obs      (obs) int64 0 1 2 3 4 5 6 7 8 ... 892 893 894 895 896 897 898 899
Data variables:
    y_cat    (chain, draw, obs) int64 4 1 4 4 1 1 4 1 4 3 ... 3 4 3 3 3 4 3 3 4
Attributes:
    created_at:                 2025-03-22T20:10:20.511013
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:  (obs: 900)
Coordinates:
  * obs      (obs) int64 0 1 2 3 4 5 6 7 8 ... 892 893 894 895 896 897 898 899
Data variables:
    y_cat    (obs) int64 2 2 2 1 1 2 2 2 2 2 2 2 2 ... 2 2 2 2 2 2 2 1 2 2 2 2 2
Attributes:
    created_at:                 2025-03-22T20:10:20.511656
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

summaries = az.summary(idata_m1, var_names=["beta_ic", "beta_oc"])
summaries
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta_ic -0.006 0.0 -0.007 -0.006 0.0 0.0 3325.0 2691.0 1.0
beta_oc -0.005 0.0 -0.005 -0.004 0.0 0.0 3777.0 2784.0 1.0

In the mlogit vignette they report how the above model specification leads to inadequate parameter estimates. They note for instance that while the utility scale itself is hard to interpret the value of the ratio of the coefficients is often meaningful because when:

\[ U = \beta_{oc}oc + \beta_{ic}ic \]

then the marginal rate of substitution is just the ratio of the two beta coefficients. The relative importance of one component of the utility equation to another is an economically meaningful quantity even if the notion of subjective utility is itself unobservable.

\[ dU = \beta_{ic} dic + \beta_{oc} doc = 0 \Rightarrow -\frac{dic}{doc}\mid_{dU=0}=\frac{\beta_{oc}}{\beta_{ic}}\]

Our parameter estimates differ slightly from the reported estimates, but we agree the model is inadequate. We will show a number of Bayesian model checks to demonstrate this fact, but the main call out is that the parameter values for installation costs should probably be negative. It’s counter-intuitive that a \(\beta_{ic}\) increase in price would increase the utility of generated by the installation even marginally as here. Although we might imagine that some kind of quality assurance comes with price which drives satisfaction with higher installation costs. The coefficient for repeat operating costs is negative as expected. Putting this issue aside for now, we’ll show below how we can incorporate prior knowledge to adjust for this kind of conflicts with theory.

But in any case, once we have a fitted model we can calculate the marginal rate of substitution as follows:

## marginal rate of substitution for a reduction in installation costs
post = az.extract(idata_m1)
substitution_rate = post["beta_oc"] / post["beta_ic"]
substitution_rate.mean().item()

0.7377857195962645

This statistic gives a view of the relative importance of the attributes which drive our utility measures. But being good Bayesians we actually want to calculate the posterior distribution for this statistic.

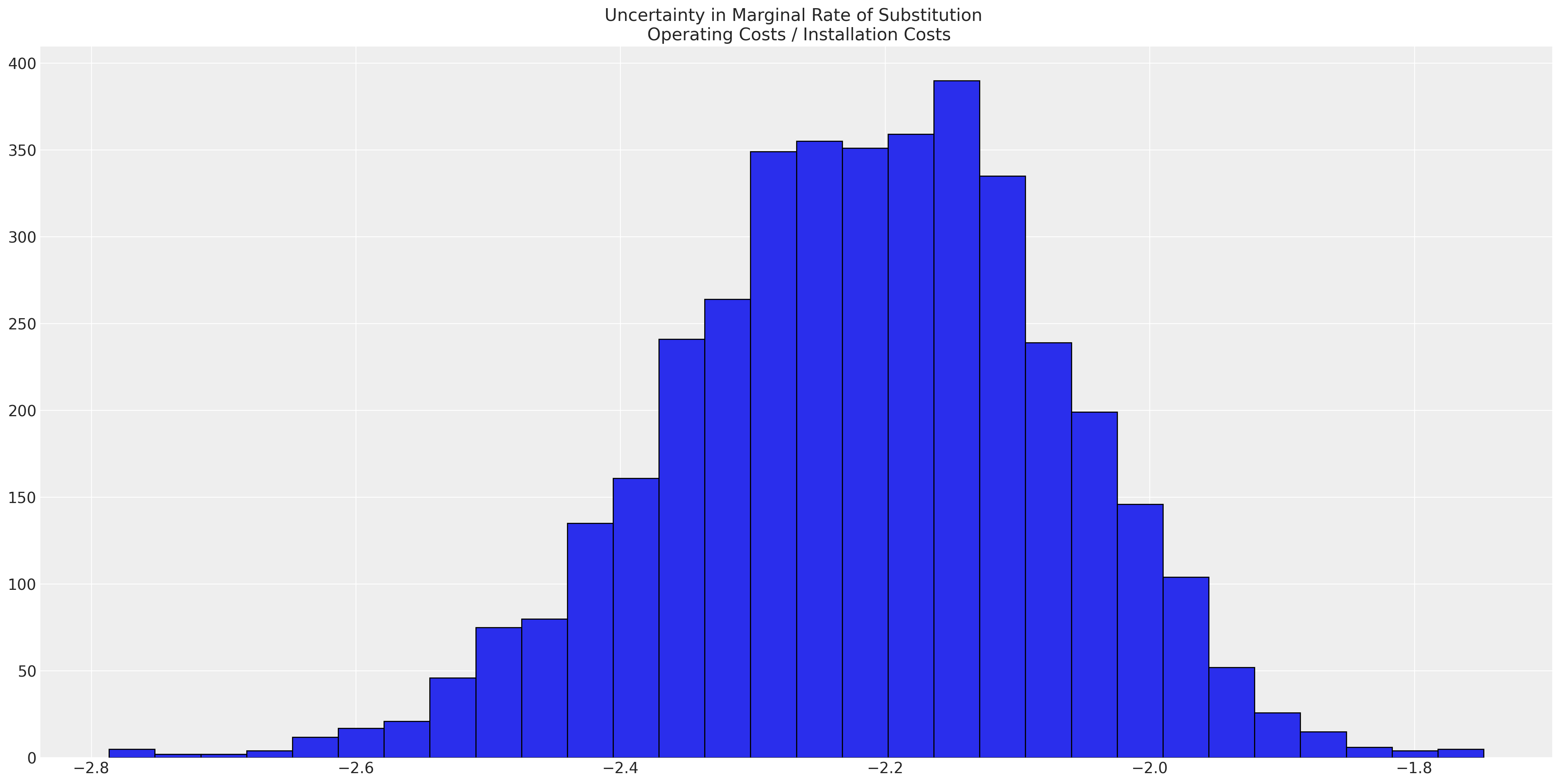
fig, ax = plt.subplots(figsize=(20, 10))

ax.hist(
    substitution_rate,
    bins=30,
    ec="black",
)
ax.set_title("Uncertainty in Marginal Rate of Substitution \n Operating Costs / Installation Costs");
../_images/f86af10a00cb684095f63377fd4851d766074c4ebeea55ae1f1e0c11927ce988.png

which suggests that there is around .7 of the value accorded to the a unit reduction in recurring operating costs over the one-off installation costs. Whether this is remotely plausible is almost beside the point since the model does not even closely capture the data generating process. But it’s worth repeating that the native scale of utility is not straightforwardly meaningful, but the ratio of the coefficients in the utility equations can be directly interpreted.

To assess overall model adequacy we can rely on the posterior predictive checks to see if the model can recover an approximation to the data generating process.

idata_m1["posterior"]["p"].mean(dim=["chain", "draw", "obs"])

<xarray.DataArray 'p' (alts_probs: 5)>
array([0.10421251, 0.05138074, 0.51701653, 0.24023285, 0.08715736])
Coordinates:
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
fig, axs = plt.subplots(1, 2, figsize=(20, 10))
ax = axs[0]
counts = wide_heating_df.groupby("depvar")["idcase"].count()
predicted_shares = idata_m1["posterior"]["p"].mean(dim=["chain", "draw", "obs"])
ci_lb = idata_m1["posterior"]["p"].quantile(0.025, dim=["chain", "draw", "obs"])
ci_ub = idata_m1["posterior"]["p"].quantile(0.975, dim=["chain", "draw", "obs"])
ax.scatter(ci_lb, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(ci_ub, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(
    counts / counts.sum(),
    ["ec", "er", "gc", "gr", "hp"],
    label="Observed Shares",
    color="red",
    s=100,
)
ax.hlines(
    ["ec", "er", "gc", "gr", "hp"], ci_lb, ci_ub, label="Predicted 95% Interval", color="black"
)
ax.legend()
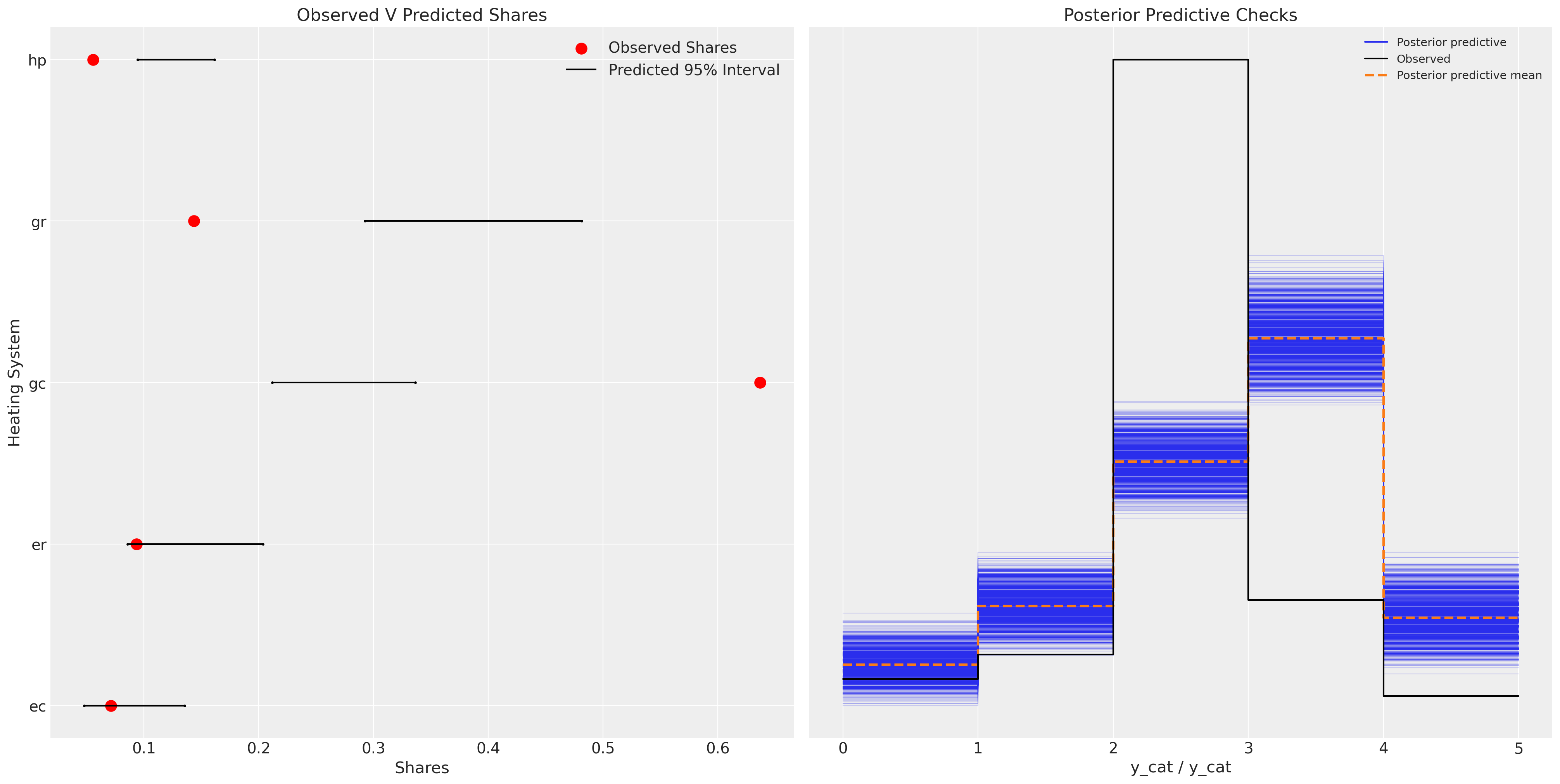
ax.set_title("Observed V Predicted Shares")
az.plot_ppc(idata_m1, ax=axs[1])
axs[1].set_title("Posterior Predictive Checks")
ax.set_xlabel("Shares")
ax.set_ylabel("Heating System");

/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:267: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten_pp = list(predictive_dataset.dims.keys())
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:271: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten = list(observed_data.dims.keys())
../_images/29cf698e8ee44806dc8594d1f987808e01b2e43dce5692377f55ff4460bb9bef.png

We can see here that the model is fairly inadequate, and fails quite dramatically to recapture the posterior predictive distribution.

Improved Model: Adding Alternative Specific Intercepts#

We can address some of the issues with the prior model specification by adding intercept terms for each of the unique alternatives gr, gc, ec, er. These terms will absorb some of the error seen in the last model by allowing us to control some of the heterogenity of utility measures across products.

N = wide_heating_df.shape[0]
observed = pd.Categorical(wide_heating_df["depvar"]).codes

coords = {
    "alts_intercepts": ["ec", "er", "gc", "gr"],
    "alts_probs": ["ec", "er", "gc", "gr", "hp"],
    "obs": range(N),
}
with pm.Model(coords=coords) as model_2:
    beta_ic = pm.Normal("beta_ic", 0, 1)
    beta_oc = pm.Normal("beta_oc", 0, 1)
    alphas = pm.Normal("alpha", 0, 1, dims="alts_intercepts")

    ## Construct Utility matrix and Pivot using an intercept per alternative
    u0 = alphas[0] + beta_ic * wide_heating_df["ic.ec"] + beta_oc * wide_heating_df["oc.ec"]
    u1 = alphas[1] + beta_ic * wide_heating_df["ic.er"] + beta_oc * wide_heating_df["oc.er"]
    u2 = alphas[2] + beta_ic * wide_heating_df["ic.gc"] + beta_oc * wide_heating_df["oc.gc"]
    u3 = alphas[3] + beta_ic * wide_heating_df["ic.gr"] + beta_oc * wide_heating_df["oc.gr"]
    u4 = 0 + beta_ic * wide_heating_df["ic.hp"] + beta_oc * wide_heating_df["oc.hp"]
    s = pm.math.stack([u0, u1, u2, u3, u4]).T

    ## Apply Softmax Transform
    p_ = pm.Deterministic("p", pm.math.softmax(s, axis=1), dims=("obs", "alts_probs"))

    ## Likelihood
    choice_obs = pm.Categorical("y_cat", p=p_, observed=observed, dims="obs")

    idata_m2 = pm.sample_prior_predictive()
    idata_m2.extend(
        pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}, random_seed=103)
    )
    idata_m2.extend(pm.sample_posterior_predictive(idata_m2))


pm.model_to_graphviz(model_2)

Sampling: [alpha, beta_ic, beta_oc, y_cat]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
  warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)

Compiling...
Compilation time =  0:00:01.074196
Sampling...

Sampling time =  0:00:12.000761
Transforming variables...
Transformation time =  0:00:00.295025
Computing Log Likelihood...

Sampling: [y_cat]

Log Likelihood time =  0:00:00.411164
100.00% [4000/4000 00:06<00:00]
../_images/4d02619a5fb389a60e511b656d1580f3ac0cebff75270357bac2709200035e57.svg

We have deliberately 0’d out the intercept parameter for the hp alternative to ensure parameter identification is feasible.

az.summary(idata_m2, var_names=["beta_ic", "beta_oc", "alpha"], round_to=4)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta_ic -0.0019 0.0006 -0.0030 -0.0007 0.0000 0.0000 2194.2030 2974.0194 1.0004
beta_oc -0.0058 0.0013 -0.0082 -0.0032 0.0000 0.0000 1317.1605 1482.4796 1.0008
alpha[ec] 1.1859 0.3856 0.4164 1.8939 0.0111 0.0079 1208.3253 1521.0849 1.0009
alpha[er] 1.4859 0.3102 0.8716 2.0489 0.0088 0.0063 1244.2319 1021.4642 1.0009
alpha[gc] 1.6028 0.2169 1.1950 2.0159 0.0060 0.0043 1319.9286 1489.0237 1.0011
alpha[gr] 0.2644 0.1925 -0.0933 0.6262 0.0051 0.0037 1408.3095 1595.1160 1.0011

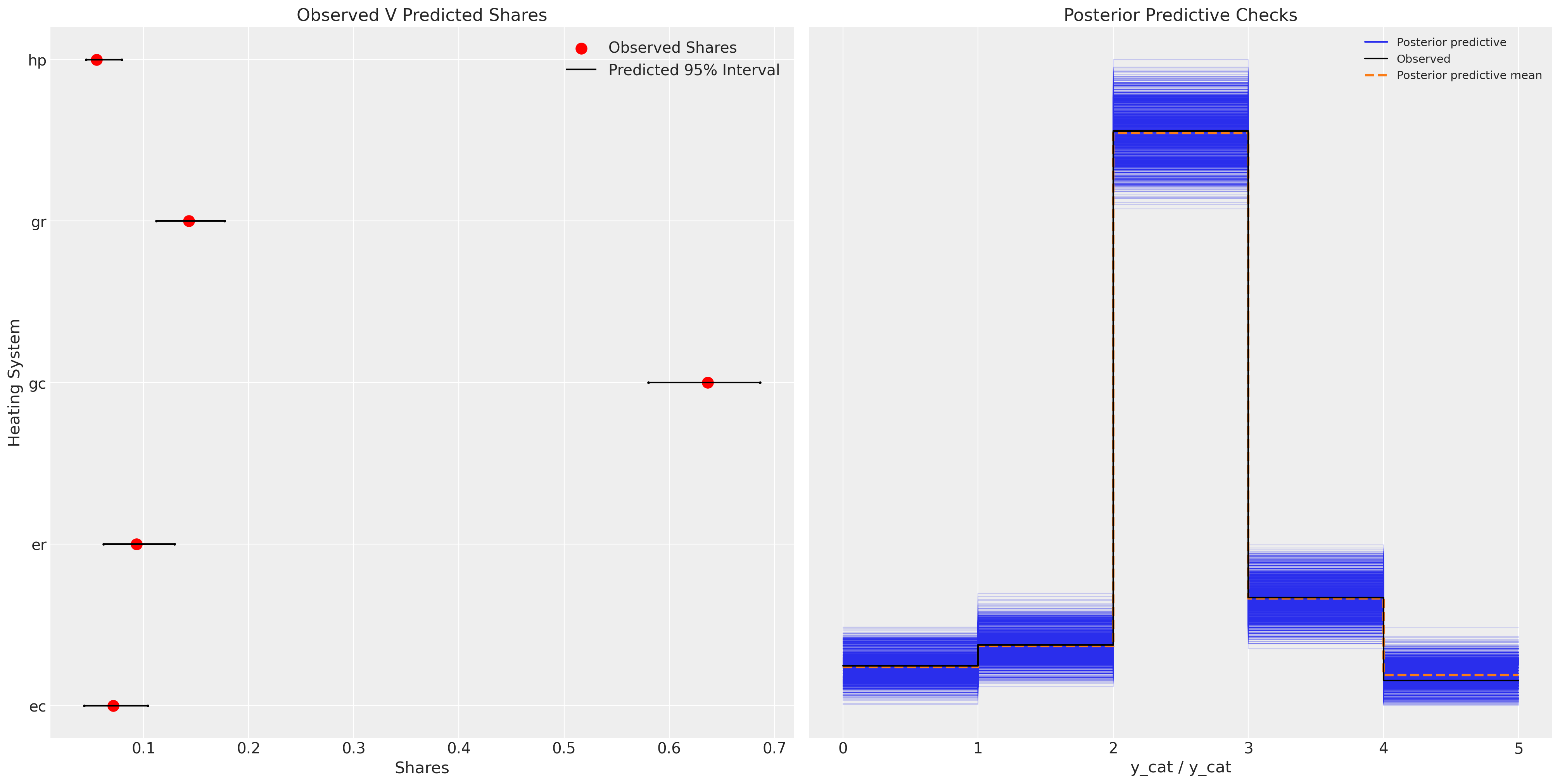
We can see now how this model performs much better in capturing aspects of the data generating process.

fig, axs = plt.subplots(1, 2, figsize=(20, 10))
ax = axs[0]
counts = wide_heating_df.groupby("depvar")["idcase"].count()
predicted_shares = idata_m2["posterior"]["p"].mean(dim=["chain", "draw", "obs"])
ci_lb = idata_m2["posterior"]["p"].quantile(0.025, dim=["chain", "draw", "obs"])
ci_ub = idata_m2["posterior"]["p"].quantile(0.975, dim=["chain", "draw", "obs"])

ax.scatter(ci_lb, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(ci_ub, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(
    counts / counts.sum(),
    ["ec", "er", "gc", "gr", "hp"],
    label="Observed Shares",
    color="red",
    s=100,
)
ax.hlines(
    ["ec", "er", "gc", "gr", "hp"], ci_lb, ci_ub, label="Predicted 95% Interval", color="black"
)
ax.legend()
ax.set_title("Observed V Predicted Shares")
az.plot_ppc(idata_m2, ax=axs[1])
axs[1].set_title("Posterior Predictive Checks")
ax.set_xlabel("Shares")
ax.set_ylabel("Heating System");

/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:267: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten_pp = list(predictive_dataset.dims.keys())
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:271: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten = list(observed_data.dims.keys())
../_images/ad1b768c5cc04bf24f69b10a8f2717bfb9522632f4ffe29f217fa76a7c912791.png

This model represents a substantial improvement.

Experimental Model: Adding Correlation Structure#

We might think that there is a correlation among the alternative goods that we should capture too. We can capture those effects in so far as they exist by placing a multvariate normal prior on the intercepts, (or alternatively the beta parameters). In addition we add information about how the effect of income influences the utility accorded to each alternative.

coords = {
    "alts_intercepts": ["ec", "er", "gc", "gr"],
    "alts_probs": ["ec", "er", "gc", "gr", "hp"],
    "obs": range(N),
}
with pm.Model(coords=coords) as model_3:
    ## Add data to experiment with changes later.
    ic_ec = pm.MutableData("ic_ec", wide_heating_df["ic.ec"])
    oc_ec = pm.MutableData("oc_ec", wide_heating_df["oc.ec"])
    ic_er = pm.MutableData("ic_er", wide_heating_df["ic.er"])
    oc_er = pm.MutableData("oc_er", wide_heating_df["oc.er"])

    beta_ic = pm.Normal("beta_ic", 0, 1)
    beta_oc = pm.Normal("beta_oc", 0, 1)
    chol, corr, stds = pm.LKJCholeskyCov(
        "chol", n=5, eta=2.0, sd_dist=pm.Exponential.dist(1.0, shape=5)
    )
    alphas = pm.MvNormal("alpha", mu=0, chol=chol, dims="alts_probs")

    u0 = alphas[0] + beta_ic * ic_ec + beta_oc * oc_ec
    u1 = alphas[1] + beta_ic * ic_er + beta_oc * oc_er
    u2 = alphas[2] + beta_ic * wide_heating_df["ic.gc"] + beta_oc * wide_heating_df["oc.gc"]
    u3 = alphas[3] + beta_ic * wide_heating_df["ic.gr"] + beta_oc * wide_heating_df["oc.gr"]
    u4 = (
        alphas[4] + beta_ic * wide_heating_df["ic.hp"] + beta_oc * wide_heating_df["oc.hp"]
    )  # pivot)
    s = pm.math.stack([u0, u1, u2, u3, u4]).T

    p_ = pm.Deterministic("p", pm.math.softmax(s, axis=1), dims=("obs", "alts_probs"))
    choice_obs = pm.Categorical("y_cat", p=p_, observed=observed, dims="obs")

    idata_m3 = pm.sample_prior_predictive()
    idata_m3.extend(
        pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}, random_seed=100)
    )
    idata_m3.extend(pm.sample_posterior_predictive(idata_m3))


pm.model_to_graphviz(model_3)

Sampling: [alpha, beta_ic, beta_oc, chol, y_cat]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
  warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)

Compiling...
Compilation time =  0:00:02.342931
Sampling...

Sampling time =  0:00:23.358412
Transforming variables...
Transformation time =  0:00:00.553256
Computing Log Likelihood...

Sampling: [y_cat]

Log Likelihood time =  0:00:00.446564
100.00% [4000/4000 00:06<00:00]
../_images/d10f02daf9a633b085b3ab32ebedcbdda5df27b05cffe583f787fb72b2608240.svg

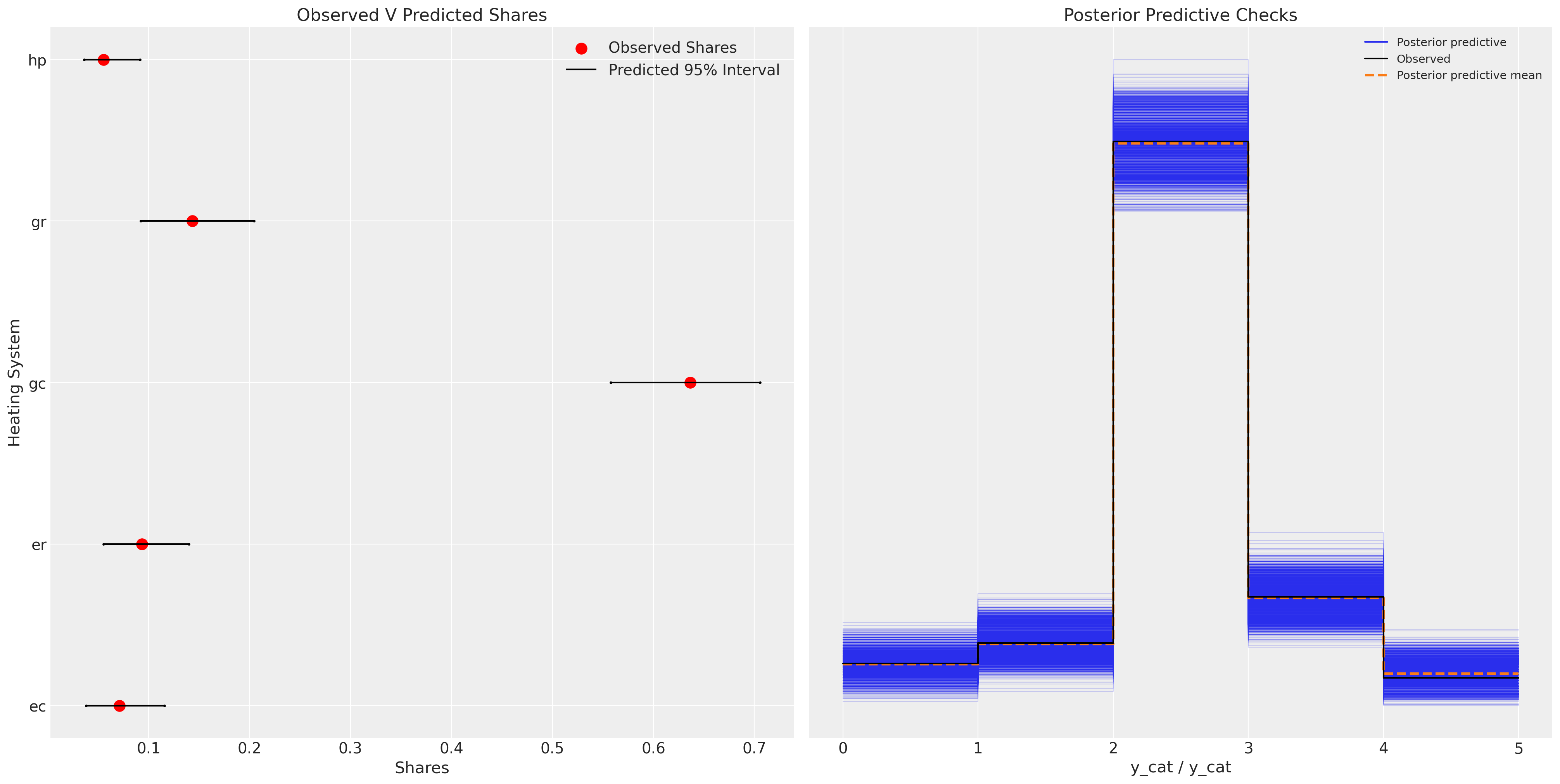
Plotting the model fit we see a similar story.The model predictive performance is not drastically improved and we have added some complexity to the model. This extra complexity ought to be penalised in model assessment metrics such as AIC and WAIC. But often the correlation amongst products are some of the features of interest, independent of issues of historic predictions.

fig, axs = plt.subplots(1, 2, figsize=(20, 10))
ax = axs[0]
counts = wide_heating_df.groupby("depvar")["idcase"].count()
predicted_shares = idata_m3["posterior"]["p"].mean(dim=["chain", "draw", "obs"])
ci_lb = idata_m3["posterior"]["p"].quantile(0.025, dim=["chain", "draw", "obs"])
ci_ub = idata_m3["posterior"]["p"].quantile(0.975, dim=["chain", "draw", "obs"])

ax.scatter(ci_lb, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(ci_ub, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(
    counts / counts.sum(),
    ["ec", "er", "gc", "gr", "hp"],
    label="Observed Shares",
    color="red",
    s=100,
)
ax.hlines(
    ["ec", "er", "gc", "gr", "hp"], ci_lb, ci_ub, label="Predicted 95% Interval", color="black"
)
ax.legend()
ax.set_title("Observed V Predicted Shares")
az.plot_ppc(idata_m3, ax=axs[1])
axs[1].set_title("Posterior Predictive Checks")
ax.set_xlabel("Shares")
ax.set_ylabel("Heating System");

/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:267: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten_pp = list(predictive_dataset.dims.keys())
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:271: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten = list(observed_data.dims.keys())
../_images/0d36b03309afe69f3f64764bcfa399f22b095a00e40943c01439c2b525fa2a14.png

That extra complexity can be informative, and the degree of relationship amongst the alternative products will inform the substitution patterns under policy changes. Also, note how under this model specification the parameter for beta_ic has a expected value of 0. Suggestive perhaps of a resignation towards the reality of installation costs that doesn’t change the utility metric one way or other after a decision to purchase.

az.summary(idata_m3, var_names=["beta_ic", "beta_oc", "alpha", "chol_corr"], round_to=4)

/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/stats/diagnostics.py:592: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta_ic -0.0016 0.0006 -0.0028 -0.0005 0.0000 0.0000 965.4150 1858.7119 1.0001
beta_oc -0.0063 0.0014 -0.0088 -0.0035 0.0001 0.0001 279.5321 415.1640 1.0173
alpha[ec] 0.1390 0.4889 -0.6647 1.2387 0.0379 0.0268 231.0307 299.2109 1.0194
alpha[er] 0.3534 0.5002 -0.2853 1.5779 0.0414 0.0293 194.8276 248.4286 1.0183
alpha[gc] 0.3954 0.5681 -0.3446 1.5776 0.0532 0.0380 112.9666 358.4609 1.0290
alpha[gr] -0.9796 0.5950 -1.8111 0.1638 0.0579 0.0410 105.7955 427.4041 1.0316
alpha[hp] -1.3157 0.5856 -2.1852 -0.1067 0.0539 0.0382 141.3095 215.2878 1.0236
chol_corr[0, 0] 1.0000 0.0000 1.0000 1.0000 0.0000 0.0000 4000.0000 4000.0000 NaN
chol_corr[0, 1] 0.0324 0.3416 -0.5952 0.6568 0.0087 0.0077 1546.9802 1197.8477 1.0018
chol_corr[0, 2] 0.0061 0.3520 -0.6189 0.6374 0.0157 0.0111 825.6169 1945.6811 1.0142
chol_corr[0, 3] 0.0092 0.3332 -0.5888 0.6468 0.0077 0.0069 1890.5246 1531.3933 1.0180
chol_corr[0, 4] 0.0476 0.3611 -0.6530 0.5964 0.0439 0.0312 69.4621 1858.2409 1.0408
chol_corr[1, 0] 0.0324 0.3416 -0.5952 0.6568 0.0087 0.0077 1546.9802 1197.8477 1.0018
chol_corr[1, 1] 1.0000 0.0000 1.0000 1.0000 0.0000 0.0000 1802.6889 1658.0984 1.0002
chol_corr[1, 2] 0.0341 0.3451 -0.5745 0.6690 0.0180 0.0127 440.1281 2672.0734 1.0144
chol_corr[1, 3] -0.0490 0.3437 -0.6373 0.6208 0.0118 0.0084 1201.2989 1567.5346 1.0077
chol_corr[1, 4] -0.0750 0.3409 -0.6803 0.5525 0.0106 0.0075 1284.5413 1900.4899 1.0091
chol_corr[2, 0] 0.0061 0.3520 -0.6189 0.6374 0.0157 0.0111 825.6169 1945.6811 1.0142
chol_corr[2, 1] 0.0341 0.3451 -0.5745 0.6690 0.0180 0.0127 440.1281 2672.0734 1.0144
chol_corr[2, 2] 1.0000 0.0000 1.0000 1.0000 0.0000 0.0000 2150.3579 3042.5649 1.0008
chol_corr[2, 3] -0.0517 0.3398 -0.6596 0.5873 0.0163 0.0115 515.9573 2505.1328 1.0134
chol_corr[2, 4] -0.0264 0.3375 -0.6438 0.5736 0.0174 0.0123 456.2480 2197.2798 1.0154
chol_corr[3, 0] 0.0092 0.3332 -0.5888 0.6468 0.0077 0.0069 1890.5246 1531.3933 1.0180
chol_corr[3, 1] -0.0490 0.3437 -0.6373 0.6208 0.0118 0.0084 1201.2989 1567.5346 1.0077
chol_corr[3, 2] -0.0517 0.3398 -0.6596 0.5873 0.0163 0.0115 515.9573 2505.1328 1.0134
chol_corr[3, 3] 1.0000 0.0000 1.0000 1.0000 0.0000 0.0000 3216.9877 3379.4979 1.0047
chol_corr[3, 4] 0.1003 0.3591 -0.4994 0.7509 0.0573 0.0408 43.4352 336.8334 1.0650
chol_corr[4, 0] 0.0476 0.3611 -0.6530 0.5964 0.0439 0.0312 69.4621 1858.2409 1.0408
chol_corr[4, 1] -0.0750 0.3409 -0.6803 0.5525 0.0106 0.0075 1284.5413 1900.4899 1.0091
chol_corr[4, 2] -0.0264 0.3375 -0.6438 0.5736 0.0174 0.0123 456.2480 2197.2798 1.0154
chol_corr[4, 3] 0.1003 0.3591 -0.4994 0.7509 0.0573 0.0408 43.4352 336.8334 1.0650
chol_corr[4, 4] 1.0000 0.0000 1.0000 1.0000 0.0000 0.0000 1901.4003 2561.2466 1.0022

In this model we see that the marginal rate of substitution shows that an increase of one dollar for the operating costs is almost 17 times more impactful on the utility calculus than a similar increase in installation costs. Which makes sense in so far as we can expect the installation costs to be a one-off expense we’re pretty resigned to.

post = az.extract(idata_m3)
substitution_rate = post["beta_oc"] / post["beta_ic"]
substitution_rate.mean().item()

4.312409953314165

Market Inteventions and Predicting Market Share#

We can additionally use these kinds of models to predict market share under interventions where we change the price offering.

with model_3:
    # update values of predictors with new 20% price increase in operating costs for electrical options
    pm.set_data({"oc_ec": wide_heating_df["oc.ec"] * 1.2, "oc_er": wide_heating_df["oc.er"] * 1.2})
    # use the updated values and predict outcomes and probabilities:
    idata_new_policy = pm.sample_posterior_predictive(
        idata_m3,
        var_names=["p", "y_cat"],
        return_inferencedata=True,
        predictions=True,
        extend_inferencedata=False,
        random_seed=100,
    )

idata_new_policy

Sampling: [y_cat]
100.00% [4000/4000 00:07<00:00]
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:     (chain: 4, draw: 1000, obs: 900, alts_probs: 5)
Coordinates:
  * chain       (chain) int64 0 1 2 3
  * draw        (draw) int64 0 1 2 3 4 5 6 7 ... 992 993 994 995 996 997 998 999
  * obs         (obs) int64 0 1 2 3 4 5 6 7 ... 892 893 894 895 896 897 898 899
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
Data variables:
    p           (chain, draw, obs, alts_probs) float64 0.03931 ... 0.05623
    y_cat       (chain, draw, obs) int64 2 4 4 2 1 2 2 2 2 ... 2 4 3 3 2 2 2 4 2
Attributes:
    created_at:                 2025-03-22T20:11:54.000714
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:      (ic_ec_dim_0: 900, oc_ec_dim_0: 900, ic_er_dim_0: 900,
                  oc_er_dim_0: 900)
Coordinates:
  * ic_ec_dim_0  (ic_ec_dim_0) int64 0 1 2 3 4 5 6 ... 894 895 896 897 898 899
  * oc_ec_dim_0  (oc_ec_dim_0) int64 0 1 2 3 4 5 6 ... 894 895 896 897 898 899
  * ic_er_dim_0  (ic_er_dim_0) int64 0 1 2 3 4 5 6 ... 894 895 896 897 898 899
  * oc_er_dim_0  (oc_er_dim_0) int64 0 1 2 3 4 5 6 ... 894 895 896 897 898 899
Data variables:
    ic_ec        (ic_ec_dim_0) float64 859.9 796.8 719.9 ... 842.8 799.8 967.9
    oc_ec        (oc_ec_dim_0) float64 664.0 624.3 526.9 ... 574.6 594.2 622.4
    ic_er        (ic_er_dim_0) float64 995.8 894.7 900.1 ... 1.123e+03 1.092e+03
    oc_er        (oc_er_dim_0) float64 606.7 583.8 485.7 ... 538.3 481.9 550.2
Attributes:
    created_at:                 2025-03-22T20:11:54.004944
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

# Old Policy Expectations
old = idata_m3["posterior"]["p"].mean(dim=["chain", "draw", "obs"])
old

<xarray.DataArray 'p' (alts_probs: 5)>
array([0.07133772, 0.09128577, 0.63642949, 0.14428672, 0.05666029])
Coordinates:
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
# New Policy Expectations
new = idata_new_policy["predictions"]["p"].mean(dim=["chain", "draw", "obs"])
new

<xarray.DataArray 'p' (alts_probs: 5)>
array([0.04381375, 0.05912996, 0.68165693, 0.15463743, 0.06076193])
Coordinates:
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
new - old

<xarray.DataArray 'p' (alts_probs: 5)>
array([-0.02752397, -0.03215581,  0.04522743,  0.01035071,  0.00410164])
Coordinates:
  * alts_probs  (alts_probs) <U2 'ec' 'er' 'gc' 'gr' 'hp'
fig, ax = plt.subplots(1, figsize=(20, 10))
counts = wide_heating_df.groupby("depvar")["idcase"].count()
new_predictions = idata_new_policy["predictions"]["p"].mean(dim=["chain", "draw", "obs"]).values
ci_lb = idata_m3["posterior"]["p"].quantile(0.025, dim=["chain", "draw", "obs"])
ci_ub = idata_m3["posterior"]["p"].quantile(0.975, dim=["chain", "draw", "obs"])
ax.scatter(ci_lb, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(ci_ub, ["ec", "er", "gc", "gr", "hp"], color="k", s=2)
ax.scatter(
    new_predictions,
    ["ec", "er", "gc", "gr", "hp"],
    color="green",
    label="New Policy Predicted Share",
    s=100,
)
ax.scatter(
    counts / counts.sum(),
    ["ec", "er", "gc", "gr", "hp"],
    label="Observed Shares",
    color="red",
    s=100,
)
ax.hlines(
    ["ec", "er", "gc", "gr", "hp"],
    ci_lb,
    ci_ub,
    label="Predicted 95% Credible Interval Old Policy",
    color="black",
)
ax.set_title("Predicted Market Shares under Old and New Pricing Policy", fontsize=20)
ax.set_xlabel("Market Share")
ax.legend();
../_images/c7d99d3dd86ed2b84845266fed1903add230299af2122a67ea7f35b9149a7da6.png

Here we can, as expected, see that a rise in the operating costs of the electrical options has a negative impact on their predicted market share.

Compare Models#

We’ll now evaluate all three model fits on their predictive performance. Predictive performance on the original data is a good benchmark that the model has appropriately captured the data generating process. But it is not (as we’ve seen) the only feature of interest in these models. These models are sensetive to our theoretical beliefs about the agents making the decisions, the view of the decision process and the elements of the choice scenario.

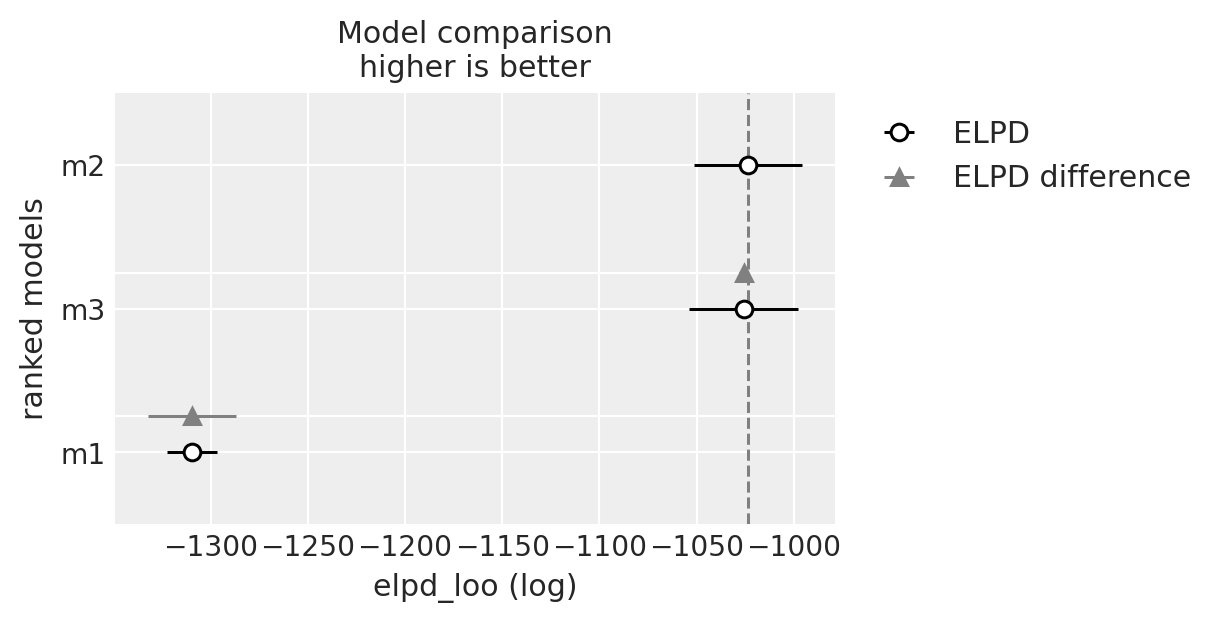
compare = az.compare({"m1": idata_m1, "m2": idata_m2, "m3": idata_m3})
compare
rank elpd_loo p_loo elpd_diff weight se dse warning scale
m3 0 -1014.070339 5.636640 0.000000 1.000000e+00 27.994286 0.000000 False log
m2 1 -1014.343946 5.398733 0.273607 1.067993e-10 27.880217 0.733146 False log
m1 2 -1097.230815 1.999354 83.160476 0.000000e+00 26.259507 12.010909 False log 
az.plot_compare(compare);
../_images/2a2e9589a77e9b78240ea3f6b0e0cf591a728c0c5db784479e3c33563b9fc002.png

Choosing Crackers over Repeated Choices: Mixed Logit Model#

Moving to another example, we see a choice scenario where the same individual has been repeatedly polled on their choice of crackers among alternatives. This affords us the opportunity to evaluate the preferences of individuals by adding in coefficients for individuals for each product.

try:
    c_df = pd.read_csv("../data/cracker_choice_short.csv")
except:
    c_df = pd.read_csv(pm.get_data("cracker_choice_short.csv"))
columns = [c for c in c_df.columns if c != "Unnamed: 0"]
c_df[columns]
personId disp.sunshine disp.keebler disp.nabisco disp.private feat.sunshine feat.keebler feat.nabisco feat.private price.sunshine price.keebler price.nabisco price.private choice lastChoice personChoiceId choiceId
0 1 0 0 0 0 0 0 0 0 0.99 1.09 0.99 0.71 nabisco nabisco 1 1
1 1 1 0 0 0 0 0 0 0 0.49 1.09 1.09 0.78 sunshine nabisco 2 2
2 1 0 0 0 0 0 0 0 0 1.03 1.09 0.89 0.78 nabisco sunshine 3 3
3 1 0 0 0 0 0 0 0 0 1.09 1.09 1.19 0.64 nabisco nabisco 4 4
4 1 0 0 0 0 0 0 0 0 0.89 1.09 1.19 0.84 nabisco nabisco 5 5
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3151 136 0 0 0 0 0 0 0 0 1.09 1.19 0.99 0.55 private private 9 3152
3152 136 0 0 0 1 0 0 0 0 0.78 1.35 1.04 0.65 private private 10 3153
3153 136 0 0 0 0 0 0 0 0 1.09 1.17 1.29 0.59 private private 11 3154
3154 136 0 0 0 0 0 0 0 0 1.09 1.22 1.29 0.59 private private 12 3155
3155 136 0 0 0 0 0 0 0 0 1.29 1.04 1.23 0.59 private private 13 3156

3156 rows × 17 columns

c_df.groupby("personId")[["choiceId"]].count().T
personId 1 2 3 4 5 6 7 8 9 10 ... 127 128 129 130 131 132 133 134 135 136
choiceId 15 15 13 28 13 27 16 25 18 40 ... 17 25 31 31 29 21 26 13 14 13

1 rows × 136 columns

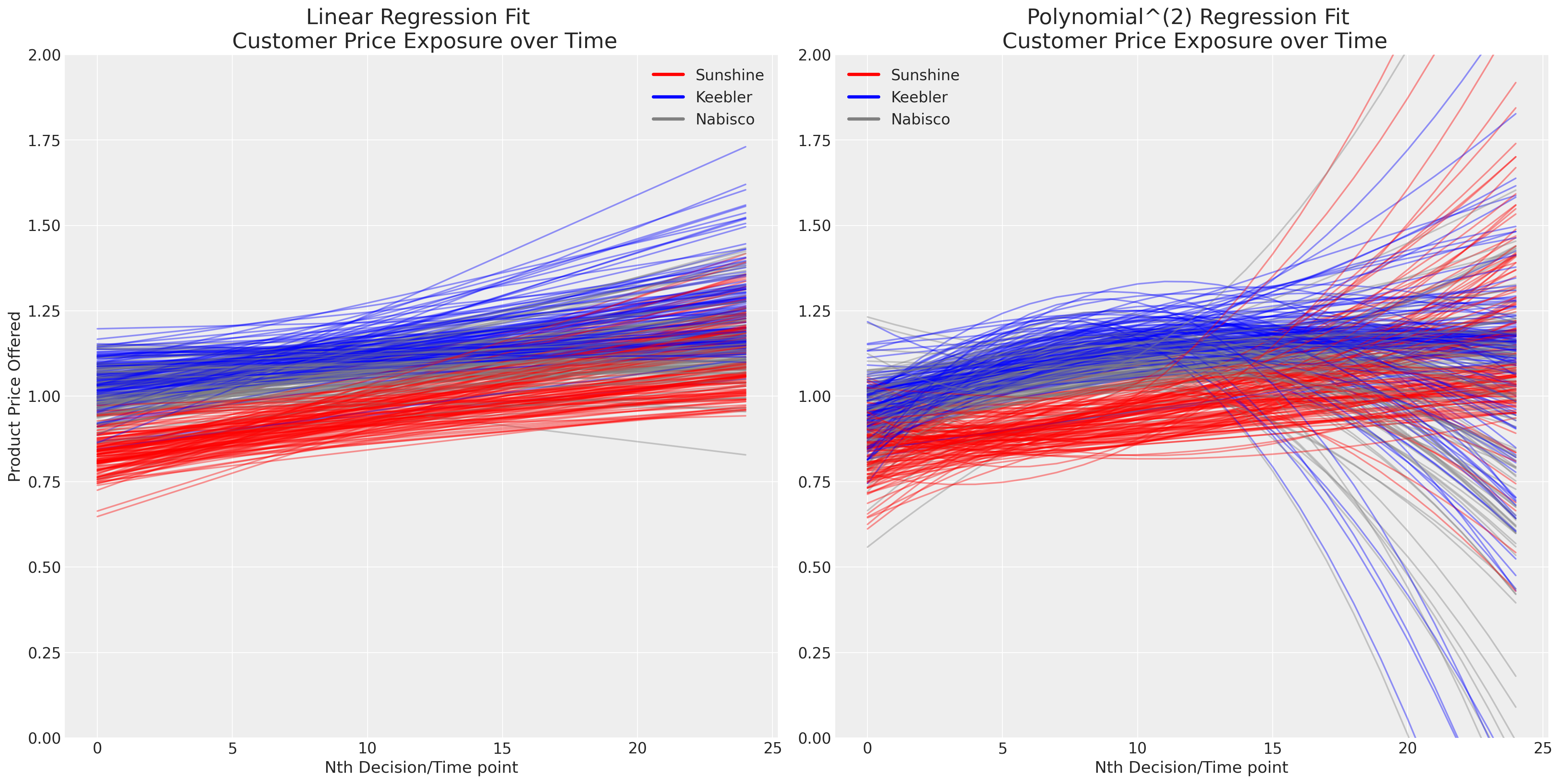
The presence of repeated choice over time complicates the issue. We now have to contend with issues of personal taste and the evolving or dynamic effects of pricing in a competitive environment. Plotting the simple linear and polynomial fits for each person’s successive exposure to the brand price, seems to suggest that (a) pricing differentiates the product offering and (b) pricing evolves over time.

fig, axs = plt.subplots(1, 2, figsize=(20, 10))
axs = axs.flatten()
map_color = {"nabisco": "red", "keebler": "blue", "sunshine": "purple", "private": "orange"}


for i in c_df["personId"].unique():
    temp = c_df[c_df["personId"] == i].copy(deep=True)
    temp["color"] = temp["choice"].map(map_color)
    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.sunshine"], deg=1))
    axs[0].plot(predict(range(25)), color="red", label="Sunshine", alpha=0.4)
    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.keebler"], deg=1))
    axs[0].plot(predict(range(25)), color="blue", label="Keebler", alpha=0.4)
    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.nabisco"], deg=1))
    axs[0].plot(predict(range(25)), color="grey", label="Nabisco", alpha=0.4)

    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.sunshine"], deg=2))
    axs[1].plot(predict(range(25)), color="red", label="Sunshine", alpha=0.4)
    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.keebler"], deg=2))
    axs[1].plot(predict(range(25)), color="blue", label="Keebler", alpha=0.4)
    predict = np.poly1d(np.polyfit(temp["personChoiceId"], temp["price.nabisco"], deg=2))
    axs[1].plot(predict(range(25)), color="grey", label="Nabisco", alpha=0.4)

axs[0].set_title("Linear Regression Fit \n Customer Price Exposure over Time", fontsize=20)
axs[1].set_title("Polynomial^(2) Regression Fit \n Customer Price Exposure over Time", fontsize=20)
axs[0].set_xlabel("Nth Decision/Time point")
axs[1].set_xlabel("Nth Decision/Time point")
axs[0].set_ylabel("Product Price Offered")
axs[1].set_ylim(0, 2)
axs[0].set_ylim(0, 2)

colors = ["red", "blue", "grey"]
lines = [Line2D([0], [0], color=c, linewidth=3, linestyle="-") for c in colors]
labels = ["Sunshine", "Keebler", "Nabisco"]
axs[0].legend(lines, labels)
axs[1].legend(lines, labels);
../_images/703f36f6fa131124a2e76dad57805ac56602520dad7cd4225a5b9fb9c9cc8b18.png

We’ll model now how individual taste enters into discrete choice problems, but ignore the complexities of the time-dimension or the endogenity of price in the system. There are adaptions of the basic discrete choice model that are designed to address each of these complications. We’ll leave the temporal dynamics as a suggested exercise for the reader.

N = c_df.shape[0]
map = {"sunshine": 0, "keebler": 1, "nabisco": 2, "private": 3}
c_df["choice_encoded"] = c_df["choice"].map(map)
observed = c_df["choice_encoded"].values
person_indx, uniques = pd.factorize(c_df["personId"])

coords = {
    "alts_intercepts": ["sunshine", "keebler", "nabisco", "private"],
    "alts_probs": ["sunshine", "keebler", "nabisco", "private"],
    "individuals": uniques,
    "obs": range(N),
}
with pm.Model(coords=coords) as model_4:
    beta_feat = pm.Normal("beta_feat", 0, 1)
    beta_disp = pm.Normal("beta_disp", 0, 1)
    beta_price = pm.Normal("beta_price", 0, 1)
    alphas = pm.Normal("alpha", 0, 1, dims="alts_intercepts")
    ## Hierarchical parameters for individual taste
    beta_individual = pm.Normal("beta_individual", 0, 0.1, dims=("individuals", "alts_intercepts"))

    u0 = (
        (alphas[0] + beta_individual[person_indx, 0])
        + beta_disp * c_df["disp.sunshine"]
        + beta_feat * c_df["feat.sunshine"]
        + beta_price * c_df["price.sunshine"]
    )
    u1 = (
        (alphas[1] + beta_individual[person_indx, 1])
        + beta_disp * c_df["disp.keebler"]
        + beta_feat * c_df["feat.keebler"]
        + beta_price * c_df["price.keebler"]
    )
    u2 = (
        (alphas[2] + beta_individual[person_indx, 2])
        + beta_disp * c_df["disp.nabisco"]
        + beta_feat * c_df["feat.nabisco"]
        + beta_price * c_df["price.nabisco"]
    )
    u3 = (
        (0 + beta_individual[person_indx, 2])
        + beta_disp * c_df["disp.private"]
        + beta_feat * c_df["feat.private"]
        + beta_price * c_df["price.private"]
    )
    s = pm.math.stack([u0, u1, u2, u3]).T

    ## Apply Softmax Transform
    p_ = pm.Deterministic("p", pm.math.softmax(s, axis=1), dims=("obs", "alts_probs"))

    ## Likelihood
    choice_obs = pm.Categorical("y_cat", p=p_, observed=observed, dims="obs")

    idata_m4 = pm.sample_prior_predictive()
    idata_m4.extend(
        pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}, random_seed=103)
    )
    idata_m4.extend(pm.sample_posterior_predictive(idata_m4))


pm.model_to_graphviz(model_4)

Sampling: [alpha, beta_disp, beta_feat, beta_individual, beta_price, y_cat]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
  warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)

Compiling...
Compilation time =  0:00:01.425976
Sampling...

Sampling time =  0:00:12.028729
Transforming variables...
Transformation time =  0:00:01.427529
Computing Log Likelihood...

Sampling: [y_cat]

Log Likelihood time =  0:00:01.775443
100.00% [4000/4000 00:24<00:00]
../_images/a9ed34c6d7b8a157fc1be1f0bdd4133563ea0fc81ae3ff41501f03cf75725ebc.svg 
az.summary(idata_m4, var_names=["beta_disp", "beta_feat", "beta_price", "alpha"]).head(6)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta_disp 0.104 0.063 -0.016 0.216 0.001 0.001 5853.0 3169.0 1.00
beta_feat 0.505 0.095 0.325 0.678 0.001 0.001 4476.0 2663.0 1.00
beta_price -2.977 0.209 -3.395 -2.607 0.005 0.004 1765.0 2557.0 1.00
alpha[sunshine] -0.708 0.093 -0.883 -0.531 0.002 0.001 2493.0 2960.0 1.00
alpha[keebler] -0.231 0.120 -0.449 0.000 0.003 0.002 1974.0 2635.0 1.00
alpha[nabisco] 1.723 0.101 1.538 1.920 0.002 0.002 1752.0 2653.0 1.01

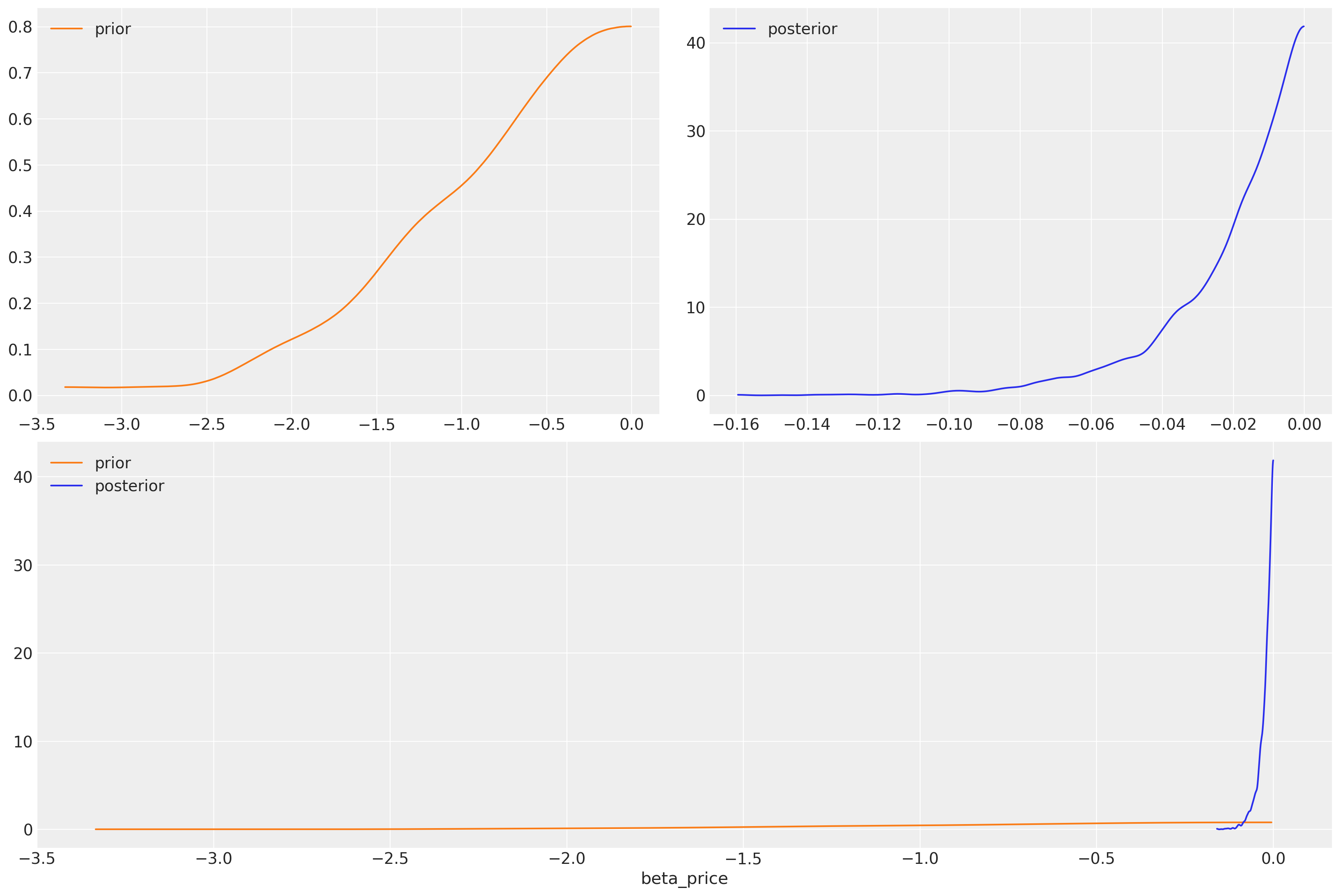
What have we learned? We’ve imposed a negative slope on the price coefficient but given it a wide prior. We can see that the data is sufficient to have narrowed the likely range of the coefficient considerably.

az.plot_dist_comparison(idata_m4, var_names=["beta_price"]);
../_images/6f443098ec76d8a35f44c5b9be934a88dbc9894f2d71fdf3bb8b3b64ae6f92f2.png

We have recovered a strongly negative estimate on the price effect in line with the basic theory of rational choice. The effect of price should have a negative impact on utility. The flexibility of priors here is key for incorporating theoretical knowledge about the process involved in choice. Priors are important for building a better picture of the decision making process and we’d be foolish to ignore their value in this setting.

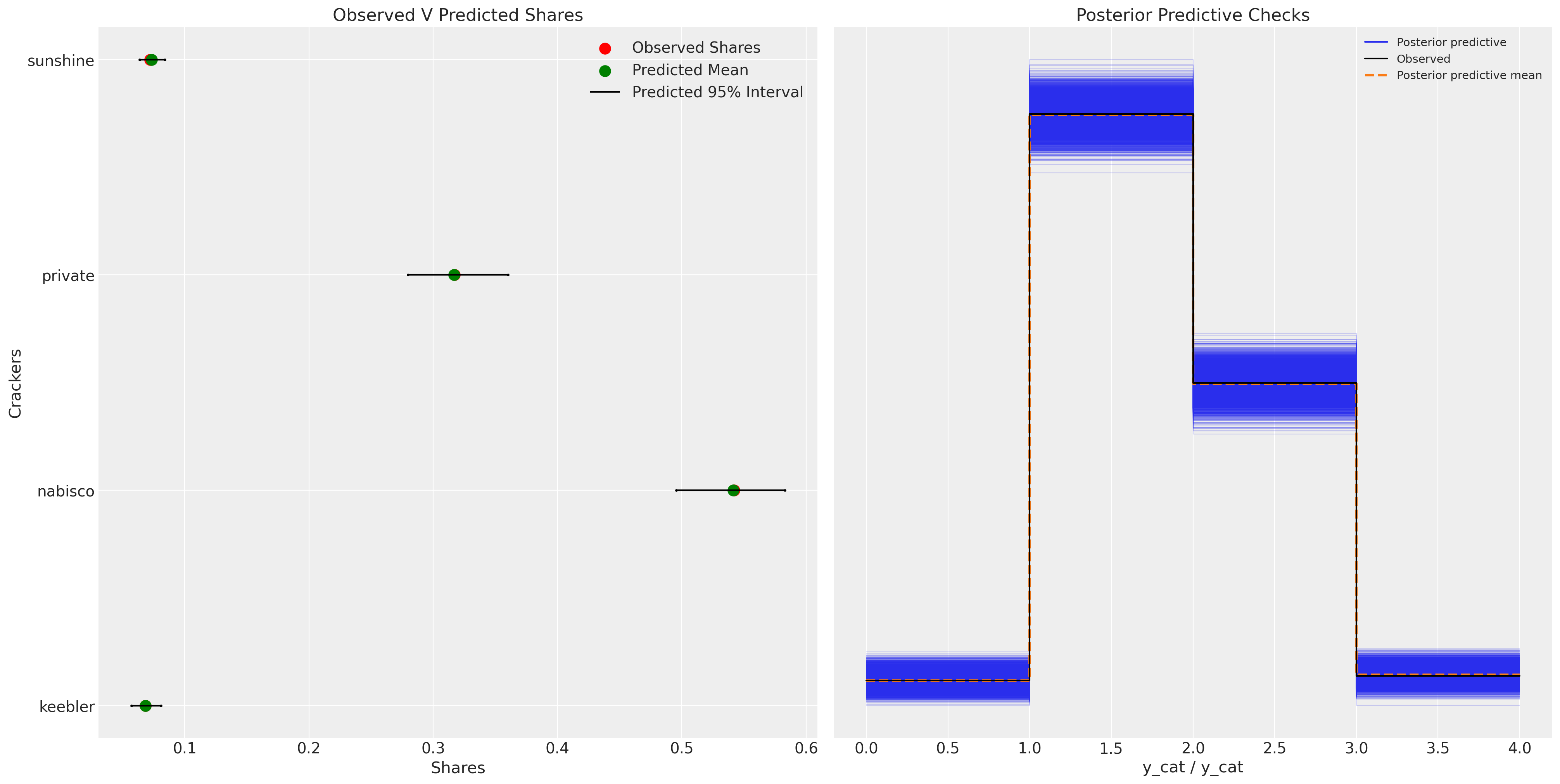
fig, axs = plt.subplots(1, 2, figsize=(20, 10))
ax = axs[0]
counts = c_df.groupby("choice")["choiceId"].count()
labels = c_df.groupby("choice")["choiceId"].count().index
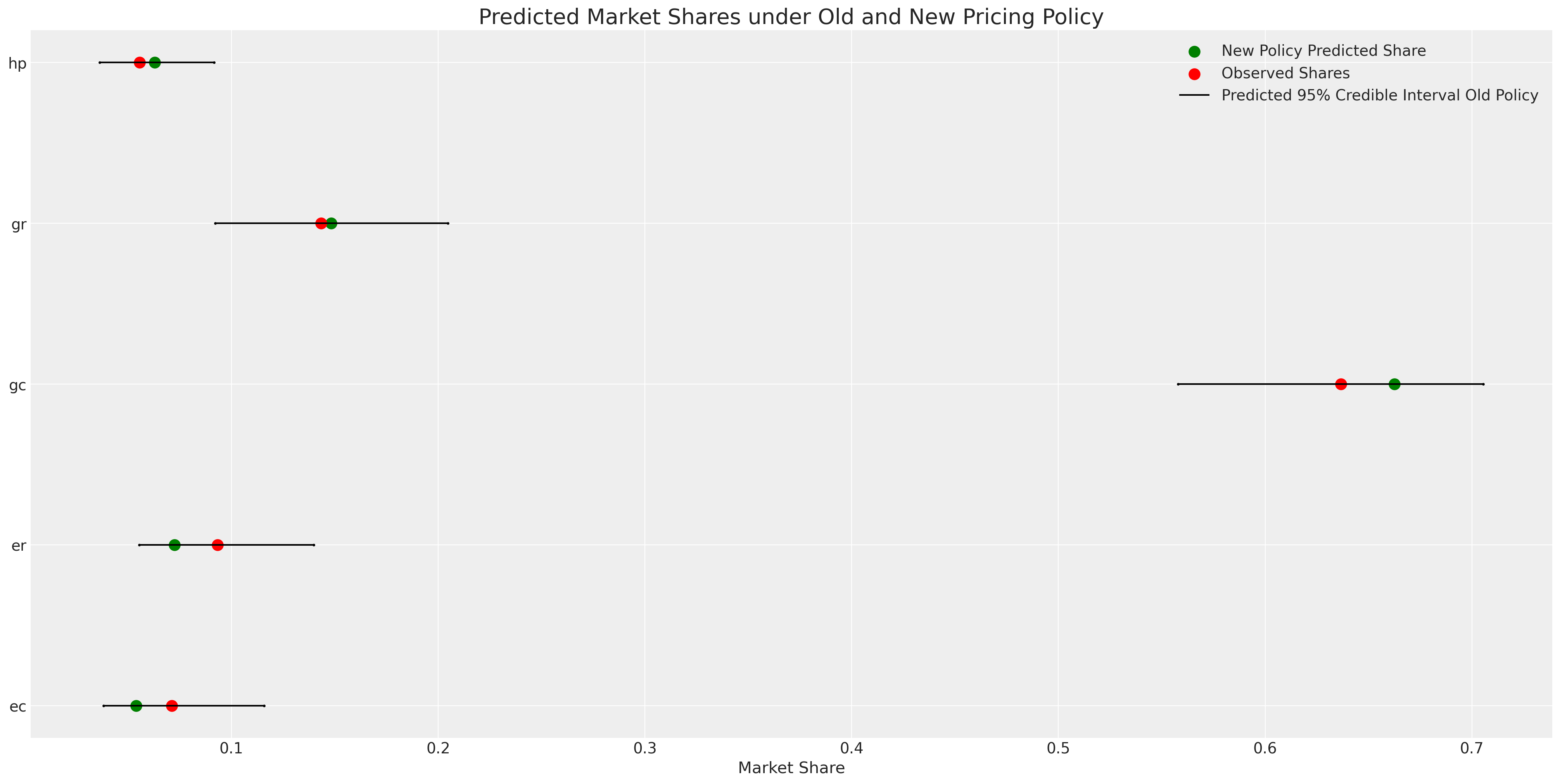
predicted_shares = idata_m4["posterior"]["p"].mean(dim=["chain", "draw", "obs"])
ci_lb = idata_m4["posterior"]["p"].quantile(0.025, dim=["chain", "draw", "obs"])
ci_ub = idata_m4["posterior"]["p"].quantile(0.975, dim=["chain", "draw", "obs"])
ax.scatter(ci_lb, labels, color="k", s=2)
ax.scatter(ci_ub, labels, color="k", s=2)
ax.scatter(
    counts / counts.sum(),
    labels,
    label="Observed Shares",
    color="red",
    s=100,
)
ax.scatter(
    predicted_shares,
    predicted_shares["alts_probs"].values,
    label="Predicted Mean",
    color="green",
    s=200,
    alpha=0.5,
)
ax.hlines(
    predicted_shares["alts_probs"].values,
    ci_lb,
    ci_ub,
    label="Predicted 95% Interval",
    color="black",
)
ax.legend()
ax.set_title("Observed V Predicted Shares")
az.plot_ppc(idata_m4, ax=axs[1])
axs[1].set_title("Posterior Predictive Checks")
ax.set_xlabel("Shares")
ax.set_ylabel("Crackers");

/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:267: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten_pp = list(predictive_dataset.dims.keys())
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/plots/ppcplot.py:271: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
  flatten = list(observed_data.dims.keys())
../_images/c11f3f7b7e46590ff4985d0f6d7bd687e98d7f7ed499ebc928d7295e165b4d40.png

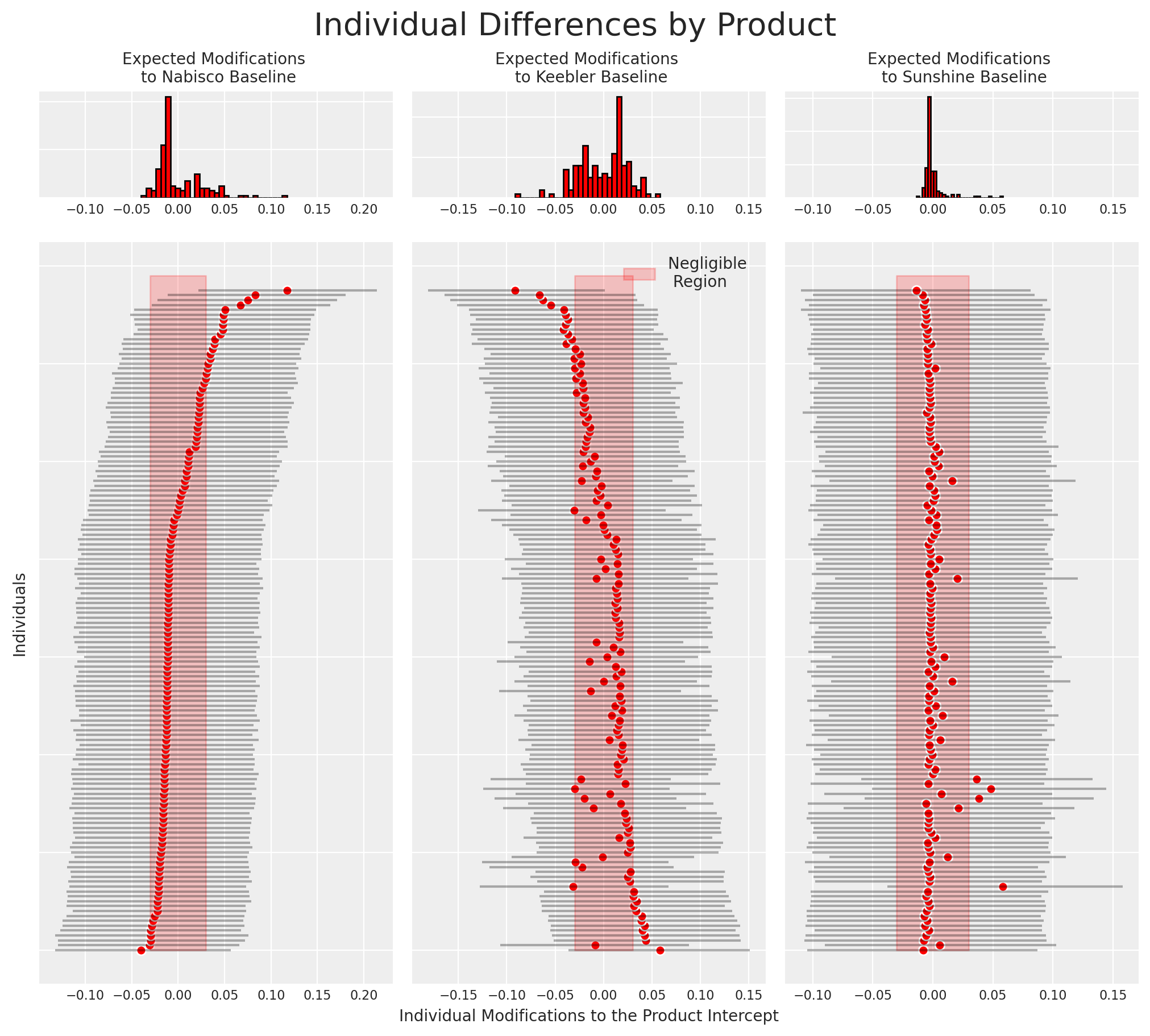
We can now also recover the differences among individuals estimated by the model for particular cracker choices. More precisely we’ll plot how the individual specific contribution to the intercept drives preferences among the cracker choices.

idata_m4
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:          (chain: 4, draw: 1000, alts_intercepts: 4,
                      individuals: 136, obs: 3156, alts_probs: 4)
Coordinates:
  * chain            (chain) int64 0 1 2 3
  * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
  * alts_intercepts  (alts_intercepts) <U8 'sunshine' 'keebler' ... 'private'
  * individuals      (individuals) int64 1 2 3 4 5 6 ... 131 132 133 134 135 136
  * obs              (obs) int64 0 1 2 3 4 5 6 ... 3150 3151 3152 3153 3154 3155
  * alts_probs       (alts_probs) <U8 'sunshine' 'keebler' 'nabisco' 'private'
Data variables:
    beta_feat        (chain, draw) float64 0.5783 0.4997 ... 0.4685 0.3407
    beta_disp        (chain, draw) float64 0.05753 0.1059 ... 0.02148 0.02866
    beta_price       (chain, draw) float64 -3.17 -3.142 -2.818 ... -2.835 -3.0
    alpha            (chain, draw, alts_intercepts) float64 -0.6961 ... 1.907
    beta_individual  (chain, draw, individuals, alts_intercepts) float64 -0.0...
    p                (chain, draw, obs, alts_probs) float64 0.05034 ... 0.4659
Attributes:
    created_at:     2025-03-22T20:12:22.857603
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:  (chain: 4, draw: 1000, obs: 3156)
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999
  * obs      (obs) int64 0 1 2 3 4 5 6 7 ... 3149 3150 3151 3152 3153 3154 3155
Data variables:
    y_cat    (chain, draw, obs) int64 2 1 2 2 0 1 2 2 3 0 ... 2 1 3 3 3 3 3 3 2
Attributes:
    created_at:                 2025-03-22T20:12:46.931302
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:      (chain: 4, draw: 1000, y_cat_dim_0: 1, y_cat_dim_1: 3156)
Coordinates:
  * chain        (chain) int64 0 1 2 3
  * draw         (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
  * y_cat_dim_0  (y_cat_dim_0) int64 0
  * y_cat_dim_1  (y_cat_dim_1) int64 0 1 2 3 4 5 ... 3151 3152 3153 3154 3155
Data variables:
    y_cat        (chain, draw, y_cat_dim_0, y_cat_dim_1) float64 -0.4611 ... ...
Attributes:
    created_at:     2025-03-22T20:12:22.862153
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:          (chain: 4, draw: 1000)
Coordinates:
  * chain            (chain) int64 0 1 2 3
  * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
Data variables:
    acceptance_rate  (chain, draw) float64 0.591 0.8318 0.8023 ... 0.9768 0.9868
    step_size        (chain, draw) float64 0.2807 0.2807 ... 0.2612 0.2612
    diverging        (chain, draw) bool False False False ... False False False
    energy           (chain, draw) float64 3.003e+03 2.971e+03 ... 3.043e+03
    n_steps          (chain, draw) int64 15 15 15 15 15 15 ... 15 15 15 15 15 15
    tree_depth       (chain, draw) int64 4 4 4 4 4 4 4 4 4 ... 4 4 4 4 4 4 4 4 4
    lp               (chain, draw) float64 2.698e+03 2.706e+03 ... 2.741e+03
Attributes:
    created_at:     2025-03-22T20:12:22.860838
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:          (chain: 1, draw: 500, alts_intercepts: 4, obs: 3156,
                      alts_probs: 4, individuals: 136)
Coordinates:
  * chain            (chain) int64 0
  * draw             (draw) int64 0 1 2 3 4 5 6 ... 493 494 495 496 497 498 499
  * alts_intercepts  (alts_intercepts) <U8 'sunshine' 'keebler' ... 'private'
  * obs              (obs) int64 0 1 2 3 4 5 6 ... 3150 3151 3152 3153 3154 3155
  * alts_probs       (alts_probs) <U8 'sunshine' 'keebler' 'nabisco' 'private'
  * individuals      (individuals) int64 1 2 3 4 5 6 ... 131 132 133 134 135 136
Data variables:
    alpha            (chain, draw, alts_intercepts) float64 1.072 ... -0.2998
    beta_price       (chain, draw) float64 -1.56 -1.028 0.3816 ... -0.5425 -1.41
    p                (chain, draw, obs, alts_probs) float64 0.4438 ... 0.5711
    beta_individual  (chain, draw, individuals, alts_intercepts) float64 -0.0...
    beta_disp        (chain, draw) float64 -0.1106 -0.604 ... 0.1959 -0.846
    beta_feat        (chain, draw) float64 1.538 0.0226 ... 0.3186 -0.3146
Attributes:
    created_at:                 2025-03-22T20:12:05.460153
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:  (chain: 1, draw: 500, obs: 3156)
Coordinates:
  * chain    (chain) int64 0
  * draw     (draw) int64 0 1 2 3 4 5 6 7 8 ... 492 493 494 495 496 497 498 499
  * obs      (obs) int64 0 1 2 3 4 5 6 7 ... 3149 3150 3151 3152 3153 3154 3155
Data variables:
    y_cat    (chain, draw, obs) int64 0 0 2 3 1 3 0 1 3 0 ... 2 3 3 1 3 1 3 3 3
Attributes:
    created_at:                 2025-03-22T20:12:05.463770
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

    • <xarray.Dataset>
Dimensions:  (obs: 3156)
Coordinates:
  * obs      (obs) int64 0 1 2 3 4 5 6 7 ... 3149 3150 3151 3152 3153 3154 3155
Data variables:
    y_cat    (obs) int64 2 0 2 2 2 0 2 2 2 2 2 2 2 ... 3 3 0 3 3 3 3 3 3 3 3 3 3
Attributes:
    created_at:                 2025-03-22T20:12:05.464353
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.3.0

beta_individual = idata_m4["posterior"]["beta_individual"]
predicted = beta_individual.mean(("chain", "draw"))
predicted = predicted.sortby(predicted.sel(alts_intercepts="nabisco"))
ci_lb = beta_individual.quantile(0.025, ("chain", "draw")).sortby(
    predicted.sel(alts_intercepts="nabisco")
)
ci_ub = beta_individual.quantile(0.975, ("chain", "draw")).sortby(
    predicted.sel(alts_intercepts="nabisco")
)

fig = plt.figure(figsize=(10, 9))
gs = fig.add_gridspec(
    2,
    3,
    width_ratios=(4, 4, 4),
    height_ratios=(1, 7),
    left=0.1,
    right=0.9,
    bottom=0.1,
    top=0.9,
    wspace=0.05,
    hspace=0.05,
)
# Create the Axes.
ax = fig.add_subplot(gs[1, 0])
ax.set_yticklabels([])
ax_histx = fig.add_subplot(gs[0, 0], sharex=ax)
ax_histx.set_title("Expected Modifications \n to Nabisco Baseline", fontsize=10)
ax_histx.hist(predicted.sel(alts_intercepts="nabisco"), bins=30, ec="black", color="red")
ax_histx.set_yticklabels([])
ax_histx.tick_params(labelsize=8)
ax.set_ylabel("Individuals", fontsize=10)
ax.tick_params(labelsize=8)
ax.hlines(
    range(len(predicted)),
    ci_lb.sel(alts_intercepts="nabisco"),
    ci_ub.sel(alts_intercepts="nabisco"),
    color="black",
    alpha=0.3,
)
ax.scatter(predicted.sel(alts_intercepts="nabisco"), range(len(predicted)), color="red", ec="white")
ax.fill_betweenx(range(139), -0.03, 0.03, alpha=0.2, color="red")

ax1 = fig.add_subplot(gs[1, 1])
ax1.set_yticklabels([])
ax_histx = fig.add_subplot(gs[0, 1], sharex=ax1)
ax_histx.set_title("Expected Modifications \n to Keebler Baseline", fontsize=10)
ax_histx.set_yticklabels([])
ax_histx.tick_params(labelsize=8)
ax_histx.hist(predicted.sel(alts_intercepts="keebler"), bins=30, ec="black", color="red")
ax1.hlines(
    range(len(predicted)),
    ci_lb.sel(alts_intercepts="keebler"),
    ci_ub.sel(alts_intercepts="keebler"),
    color="black",
    alpha=0.3,
)
ax1.scatter(
    predicted.sel(alts_intercepts="keebler"), range(len(predicted)), color="red", ec="white"
)
ax1.set_xlabel("Individual Modifications to the Product Intercept", fontsize=10)
ax1.fill_betweenx(range(139), -0.03, 0.03, alpha=0.2, color="red", label="Negligible \n Region")
ax1.tick_params(labelsize=8)
ax1.legend(fontsize=10)

ax2 = fig.add_subplot(gs[1, 2])
ax2.set_yticklabels([])
ax_histx = fig.add_subplot(gs[0, 2], sharex=ax2)
ax_histx.set_title("Expected Modifications \n to Sunshine Baseline", fontsize=10)
ax_histx.set_yticklabels([])
ax_histx.hist(predicted.sel(alts_intercepts="sunshine"), bins=30, ec="black", color="red")
ax2.hlines(
    range(len(predicted)),
    ci_lb.sel(alts_intercepts="sunshine"),
    ci_ub.sel(alts_intercepts="sunshine"),
    color="black",
    alpha=0.3,
)
ax2.fill_betweenx(range(139), -0.03, 0.03, alpha=0.2, color="red")
ax2.scatter(
    predicted.sel(alts_intercepts="sunshine"), range(len(predicted)), color="red", ec="white"
)
ax2.tick_params(labelsize=8)
ax_histx.tick_params(labelsize=8)
plt.suptitle("Individual Differences by Product", fontsize=20);
../_images/a1e07d00a0c38a1584b380b1111ff6c69f374766596f024993ac35fbb79f2dc9.png

This type of plot is often useful for identifying loyal customers. Similarly it can be used to identify cohorts of customers that ought to be better incentivised if we hope them to switch to our product.

Conclusion#

We can see here the flexibility and richly parameterised possibilities for modelling individual choice of discrete options. These techniques are useful in a wide variety of domains from microeconomics, to marketing and product development. The notions of utility, probability and their interaction lie at the heart of Savage’s Representation theorem and justification(s) for Bayesian approaches to statistical inference. So discrete modelling is a natural fit for the Bayesian, but Bayesian statistics is also a natural fit for discrete choice modelling. The traditional estimation techniques are often brittle and very dependent on starting values of the MLE process. The Bayesian setting trades this brittleness for a framework which allows us to incorporate our beliefs about what drives human utility calculations. We’ve only scratched the surface in this example notebook, but encourage you to further explore the technique.

Authors#

References#

[1] (1,2)

Kenneth Train. Discrete Choice Methods with Simulation. Cambridge, 2009.

Watermark#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Sat Mar 22 2025

Python implementation: CPython
Python version       : 3.9.16
IPython version      : 8.12.0

pytensor: 2.11.1

numpy     : 1.24.4
pytensor  : 2.11.1
pymc      : 5.3.0
matplotlib: 3.8.2
arviz     : 0.17.0
pandas    : 1.5.3

Watermark: 2.3.1

License notice#

All the notebooks in this example gallery are provided under the MIT License which allows modification, and redistribution for any use provided the copyright and license notices are preserved.

Citing PyMC examples#

To cite this notebook, use the DOI provided by Zenodo for the pymc-examples repository.

Important

Many notebooks are adapted from other sources: blogs, books… In such cases you should cite the original source as well.

Also remember to cite the relevant libraries used by your code.

Here is an citation template in bibtex:

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

which once rendered could look like:

Nathaniel Forde . "Discrete Choice and Random Utility Models". In: PyMC Examples. Ed. by PyMC Team. DOI: 10.5281/zenodo.5654871