pymc.VonMises#

class pymc.VonMises(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)[source]#

Univariate VonMises log-likelihood.

The pdf of this distribution is

\[f(x \mid \mu, \kappa) = \frac{e^{\kappa\cos(x-\mu)}}{2\pi I_0(\kappa)}\]

where \(I_0\) is the modified Bessel function of order 0.

(Source code, png, hires.png, pdf)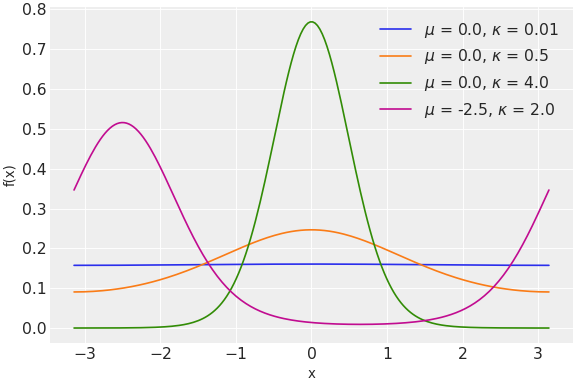

../../../_images/pymc-VonMises-1.png

Support

\(x \in [-\pi, \pi]\)

Mean

\(\mu\)

Variance

\(1-\frac{I_1(\kappa)}{I_0(\kappa)}\)
Parameters:
mutensor_like of float, default 0.0

Mean.

kappatensor_like of float, default 1.0

Concentration (\(\frac{1}{\kappa}\) is analogous to \(\sigma^2\)).

Methods

VonMises.dist([mu, kappa])

Create a tensor variable corresponding to the cls distribution.