pymc.Interpolated

class pymc.Interpolated(name, *args, rng=None, dims=None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)

Univariate linear interpolation of pdf evaluated on some lattice of points.

The lattice can be uneven, so the steps between different points can have different size and it is possible to vary the precision between regions of the support.

The probability density function values don not have to be normalized, as the interpolated density is any way normalized to make the total probability equal to $1$.

Both parameters x_points and values pdf_points are not variables, but plain array-like objects, so they are constant and cannot be sampled.

(Source code, png, hires.png, pdf)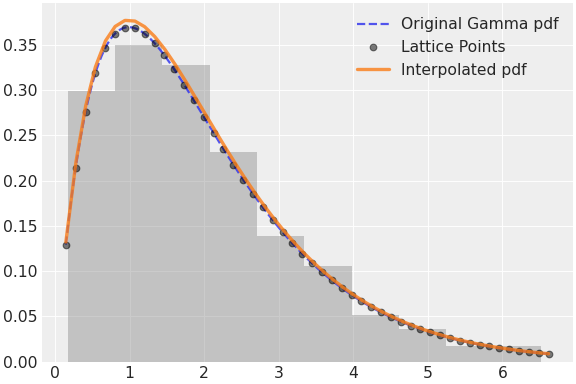

Support

\(x \in [x\_points[0], x\_points[-1]]\)

Parameters:

x_pointsarray_like

A monotonically growing list of values. Must be non-symbolic.

pdf_pointsarray_like

Probability density function evaluated on lattice x_points. Must be non-symbolic.

Methods

Interpolated.dist(x_points, pdf_points, ...)

Create a tensor variable corresponding to the cls distribution.