pymc.Bernoulli#
- class pymc.Bernoulli(name, *args, **kwargs)[source]#
Bernoulli log-likelihood
The Bernoulli distribution describes the probability of successes (x=1) and failures (x=0). The pmf of this distribution is
\[f(x \mid p) = p^{x} (1-p)^{1-x}\](
Source code,png,hires.png,pdf)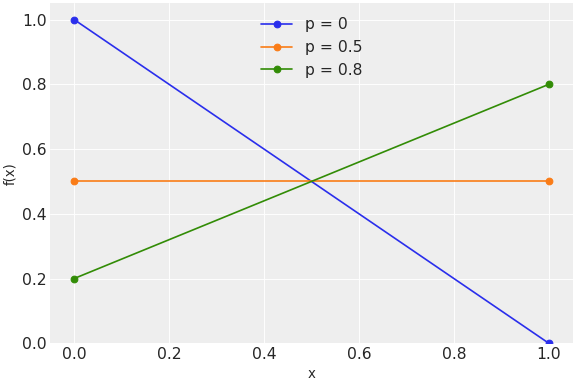
Support
\(x \in \{0, 1\}\)
Mean
\(p\)
Variance
\(p (1 - p)\)
The bernoulli distribution can be parametrized either in terms of p or logit_p. The link between the parametrizations is given by
\[logit(p) = ln(\frac{p}{1-p})\]- Parameters:
- ptensor_like of
float Probability of success (0 < p < 1).
- logit_ptensor_like of
float Alternative log odds for the probability of success.
- ptensor_like of
Methods
Bernoulli.dist([p, logit_p])Creates a tensor variable corresponding to the cls distribution.