pymc.NegativeBinomial#
- class pymc.NegativeBinomial(name, *args, **kwargs)[source]#
Negative binomial log-likelihood.
The negative binomial distribution describes a Poisson random variable whose rate parameter is gamma distributed. Its pmf, parametrized by the parameters alpha and mu of the gamma distribution, is
\[f(x \mid \mu, \alpha) = \binom{x + \alpha - 1}{x} (\alpha/(\mu+\alpha))^\alpha (\mu/(\mu+\alpha))^x\](
Source code,png,hires.png,pdf)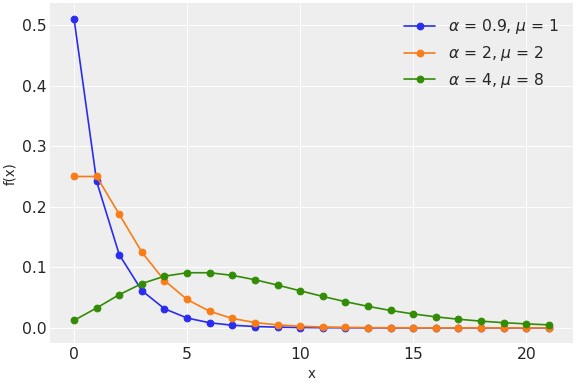
Support
\(x \in \mathbb{N}_0\)
Mean
\(\mu\)
Variance
\(\frac{\mu^2}{\alpha} + \mu\)
The negative binomial distribution can be parametrized either in terms of mu or p, and either in terms of alpha or n. The link between the parametrizations is given by
\[\begin{split}p &= \frac{\alpha}{\mu + \alpha} \\ n &= \alpha\end{split}\]If it is parametrized in terms of n and p, the negative binomial describes the probability to have x failures before the n-th success, given the probability p of success in each trial. Its pmf is
\[f(x \mid n, p) = \binom{x + n - 1}{x} (p)^n (1 - p)^x\]- Parameters:
- alphatensor_like of
float Gamma distribution shape parameter (alpha > 0).
- mutensor_like of
float Gamma distribution mean (mu > 0).
- ptensor_like of
float Alternative probability of success in each trial (0 < p < 1).
- ntensor_like of
float Alternative number of target success trials (n > 0)
- alphatensor_like of
Methods
NegativeBinomial.dist([mu, alpha, p, n])Creates a tensor variable corresponding to the cls distribution.