Inferring parameters of SDEs using a Euler-Maruyama scheme

This notebook is derived from a presentation prepared for the Theoretical Neuroscience Group, Institute of Systems Neuroscience at Aix-Marseile University.

%pylab inline
import arviz as az
import pymc3 as pm
import scipy
import theano.tensor as tt

from pymc3.distributions.timeseries import EulerMaruyama

Populating the interactive namespace from numpy and matplotlib

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

Toy model 1

Here’s a scalar linear SDE in symbolic form

\( dX_t = \lambda X_t + \sigma^2 dW_t \)

discretized with the Euler-Maruyama scheme

# parameters
λ = -0.78
σ2 = 5e-3
N = 200
dt = 1e-1

# time series
x = 0.1
x_t = []

# simulate
for i in range(N):
    x += dt * λ * x + sqrt(dt) * σ2 * randn()
    x_t.append(x)

x_t = array(x_t)

# z_t noisy observation
z_t = x_t + randn(x_t.size) * 5e-3

figure(figsize=(10, 3))
subplot(121)
plot(x_t[:30], "k", label="$x(t)$", alpha=0.5), plot(z_t[:30], "r", label="$z(t)$", alpha=0.5)
title("Transient"), legend()
subplot(122)
plot(x_t[30:], "k", label="$x(t)$", alpha=0.5), plot(z_t[30:], "r", label="$z(t)$", alpha=0.5)
title("All time")
tight_layout()

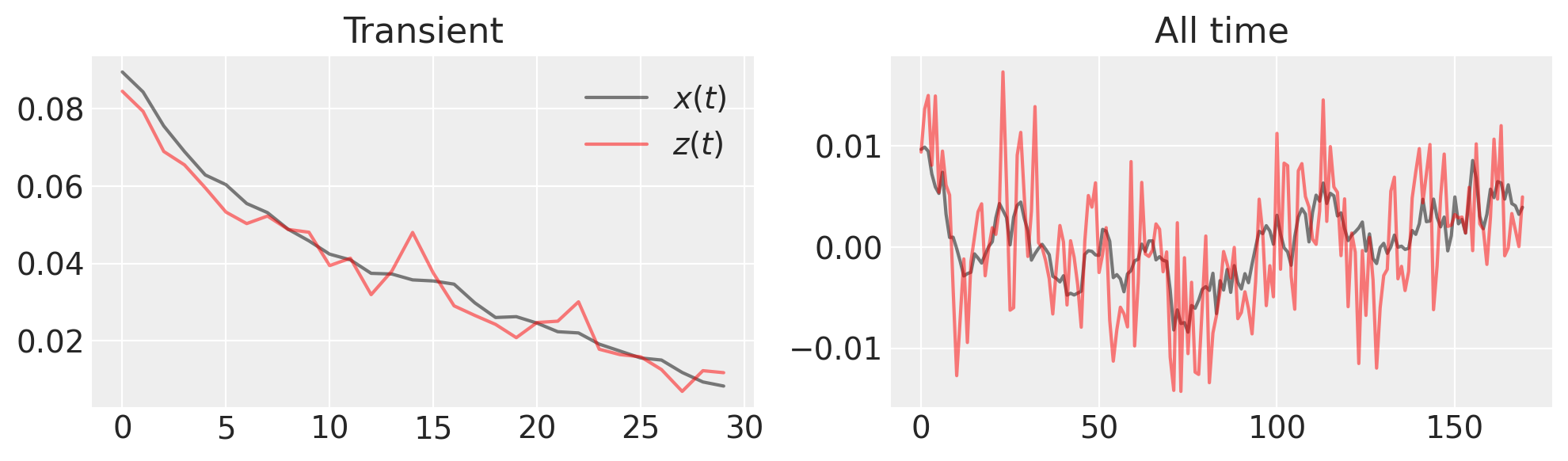
What is the inference we want to make? Since we’ve made a noisy observation of the generated time series, we need to estimate both \(x(t)\) and \(\lambda\).

First, we rewrite our SDE as a function returning a tuple of the drift and diffusion coefficients

def lin_sde(x, lam):
    return lam * x, σ2

Next, we describe the probability model as a set of three stochastic variables, lam, xh, and zh:

with pm.Model() as model:
    # uniform prior, but we know it must be negative
    lam = pm.Flat("lam")

    # "hidden states" following a linear SDE distribution
    # parametrized by time step (det. variable) and lam (random variable)
    xh = EulerMaruyama("xh", dt, lin_sde, (lam,), shape=N, testval=x_t)

    # predicted observation
    zh = pm.Normal("zh", mu=xh, sigma=5e-3, observed=z_t)

Once the model is constructed, we perform inference, i.e. sample from the posterior distribution, in the following steps:

with model:
    trace = pm.sample(2000, tune=1000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [xh, lam]

100.00% [12000/12000 00:56<00:00 Sampling 4 chains, 2,000 divergences]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 58 seconds.
The acceptance probability does not match the target. It is 0.9255362275622311, but should be close to 0.8. Try to increase the number of tuning steps.
The chain contains only diverging samples. The model is probably misspecified.
The acceptance probability does not match the target. It is 0.2038179163556457, but should be close to 0.8. Try to increase the number of tuning steps.
The rhat statistic is larger than 1.4 for some parameters. The sampler did not converge.
The estimated number of effective samples is smaller than 200 for some parameters.

Next, we plot some basic statistics on the samples from the posterior,

figure(figsize=(10, 3))
subplot(121)
plot(percentile(trace[xh], [2.5, 97.5], axis=0).T, "k", label=r"$\hat{x}_{95\%}(t)$")
plot(x_t, "r", label="$x(t)$")
legend()

subplot(122)
hist(trace[lam], 30, label=r"$\hat{\lambda}$", alpha=0.5)
axvline(λ, color="r", label=r"$\lambda$", alpha=0.5)
legend();

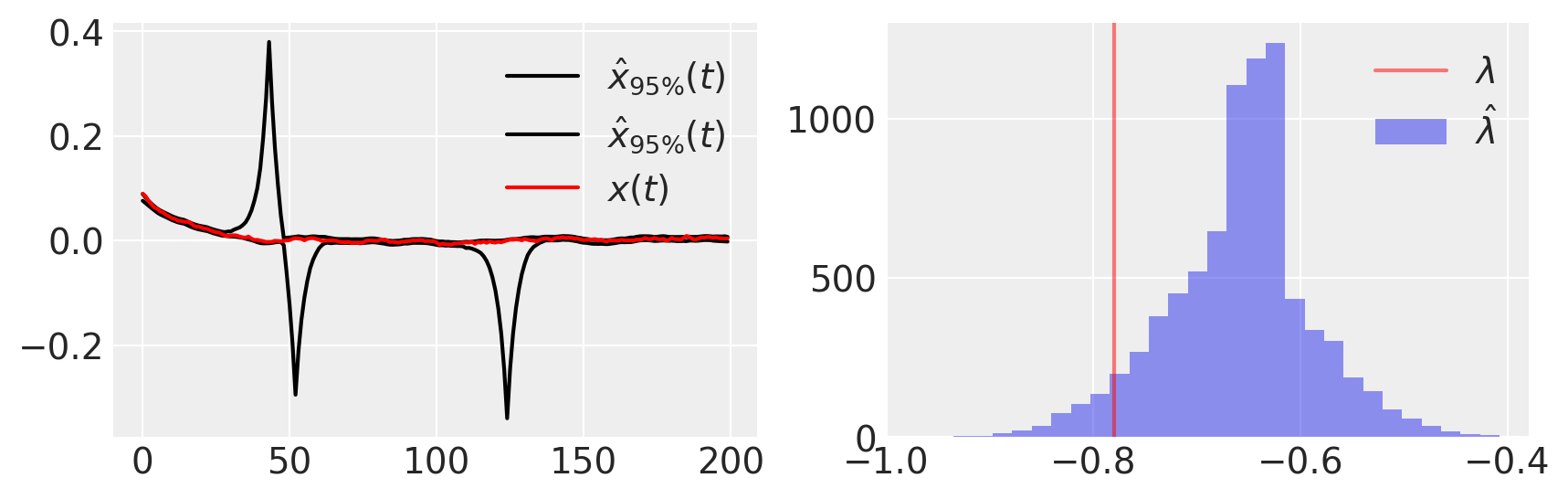
A model can fit the data precisely and still be wrong; we need to use posterior predictive checks to assess if, under our fit model, the data our likely.

In other words, we

• assume the model is correct

• simulate new observations

• check that the new observations fit with the original data

# generate trace from posterior
ppc_trace = pm.sample_posterior_predictive(trace, model=model)

# plot with data
figure(figsize=(10, 3))
plot(percentile(ppc_trace["zh"], [2.5, 97.5], axis=0).T, "k", label=r"$z_{95\% PP}(t)$")
plot(z_t, "r", label="$z(t)$")
legend()

100.00% [8000/8000 00:07<00:00]

<matplotlib.legend.Legend at 0x7f8da40af2d0>

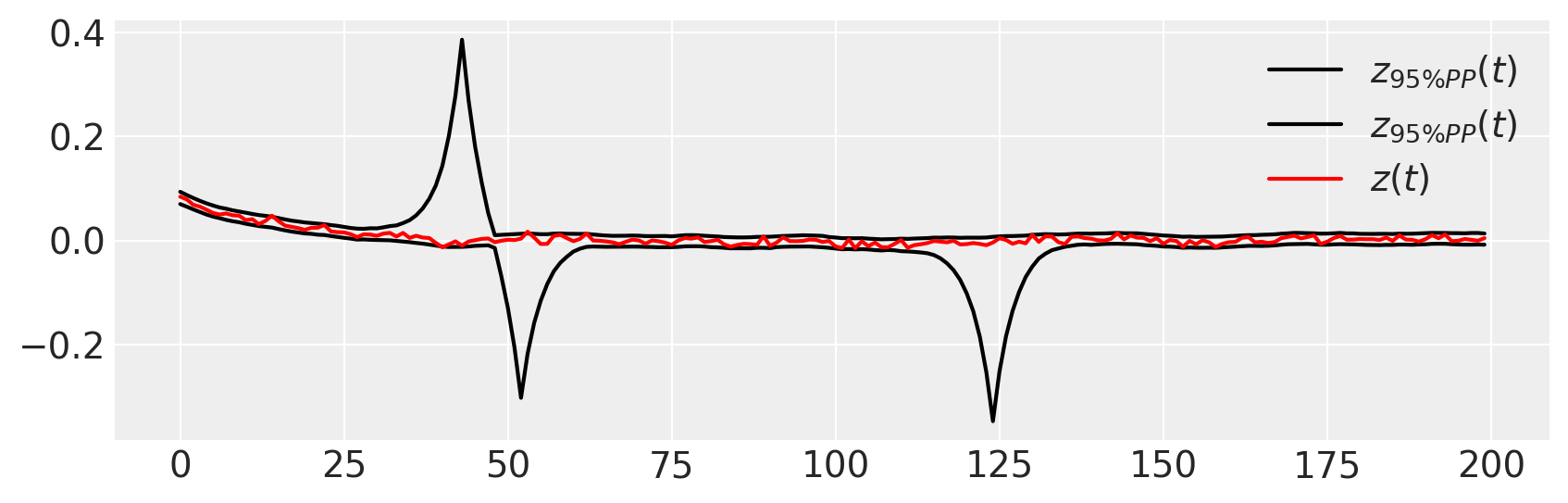
Note that

• inference also estimates the initial conditions

• the observed data \(z(t)\) lies fully within the 95% interval of the PPC.

• there are many other ways of evaluating fit

Toy model 2

As the next model, let’s use a 2D deterministic oscillator,

()\[\begin{align} \dot{x} &= \tau (x - x^3/3 + y) \\ \dot{y} &= \frac{1}{\tau} (a - x) \end{align}\]

with noisy observation \(z(t) = m x + (1 - m) y + N(0, 0.05)\).

N, τ, a, m, σ2 = 200, 3.0, 1.05, 0.2, 1e-1
xs, ys = [0.0], [1.0]
for i in range(N):
    x, y = xs[-1], ys[-1]
    dx = τ * (x - x**3.0 / 3.0 + y)
    dy = (1.0 / τ) * (a - x)
    xs.append(x + dt * dx + sqrt(dt) * σ2 * randn())
    ys.append(y + dt * dy + sqrt(dt) * σ2 * randn())
xs, ys = array(xs), array(ys)
zs = m * xs + (1 - m) * ys + randn(xs.size) * 0.1

figure(figsize=(10, 2))
plot(xs, label="$x(t)$")
plot(ys, label="$y(t)$")
plot(zs, label="$z(t)$")
legend()

<matplotlib.legend.Legend at 0x7f8da6b90fd0>

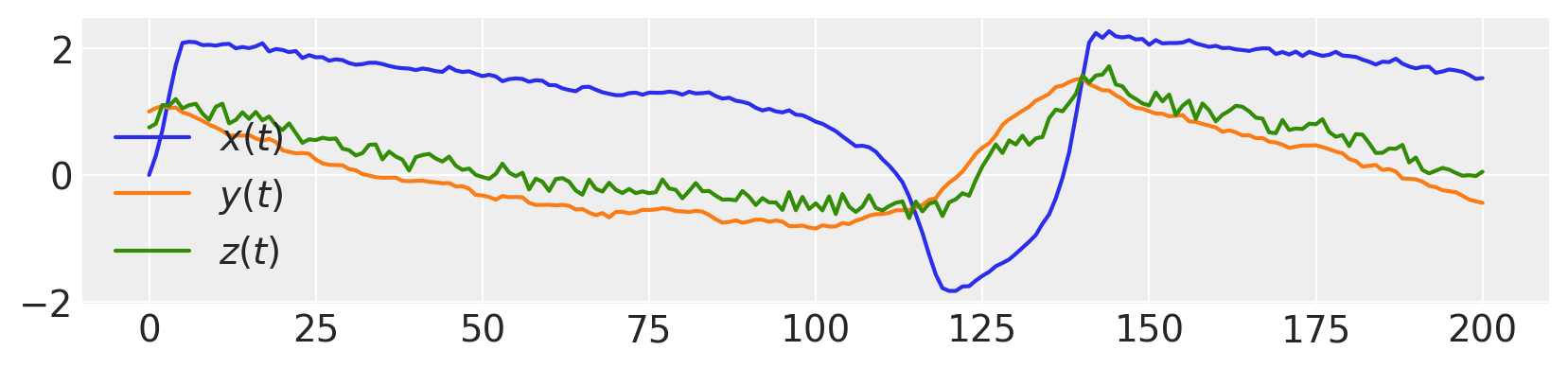
Now, estimate the hidden states \(x(t)\) and \(y(t)\), as well as parameters \(\tau\), \(a\) and \(m\).

As before, we rewrite our SDE as a function returned drift & diffusion coefficients:

def osc_sde(xy, τ, a):
    x, y = xy[:, 0], xy[:, 1]
    dx = τ * (x - x**3.0 / 3.0 + y)
    dy = (1.0 / τ) * (a - x)
    dxy = tt.stack([dx, dy], axis=0).T
    return dxy, σ2

As before, the Euler-Maruyama discretization of the SDE is written as a prediction of the state at step \(i+1\) based on the state at step \(i\).

We can now write our statistical model as before, with uninformative priors on \(\tau\), \(a\) and \(m\):

xys = c_[xs, ys]

with pm.Model() as model:
    τh = pm.Uniform("τh", lower=0.1, upper=5.0)
    ah = pm.Uniform("ah", lower=0.5, upper=1.5)
    mh = pm.Uniform("mh", lower=0.0, upper=1.0)
    xyh = EulerMaruyama("xyh", dt, osc_sde, (τh, ah), shape=xys.shape, testval=xys)
    zh = pm.Normal("zh", mu=mh * xyh[:, 0] + (1 - mh) * xyh[:, 1], sigma=0.1, observed=zs)

with model:
    trace = pm.sample(2000, tune=1000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [xyh, mh, ah, τh]

100.00% [12000/12000 02:02<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 125 seconds.
The number of effective samples is smaller than 10% for some parameters.

Again, the result is a set of samples from the posterior, including our parameters of interest but also the hidden states

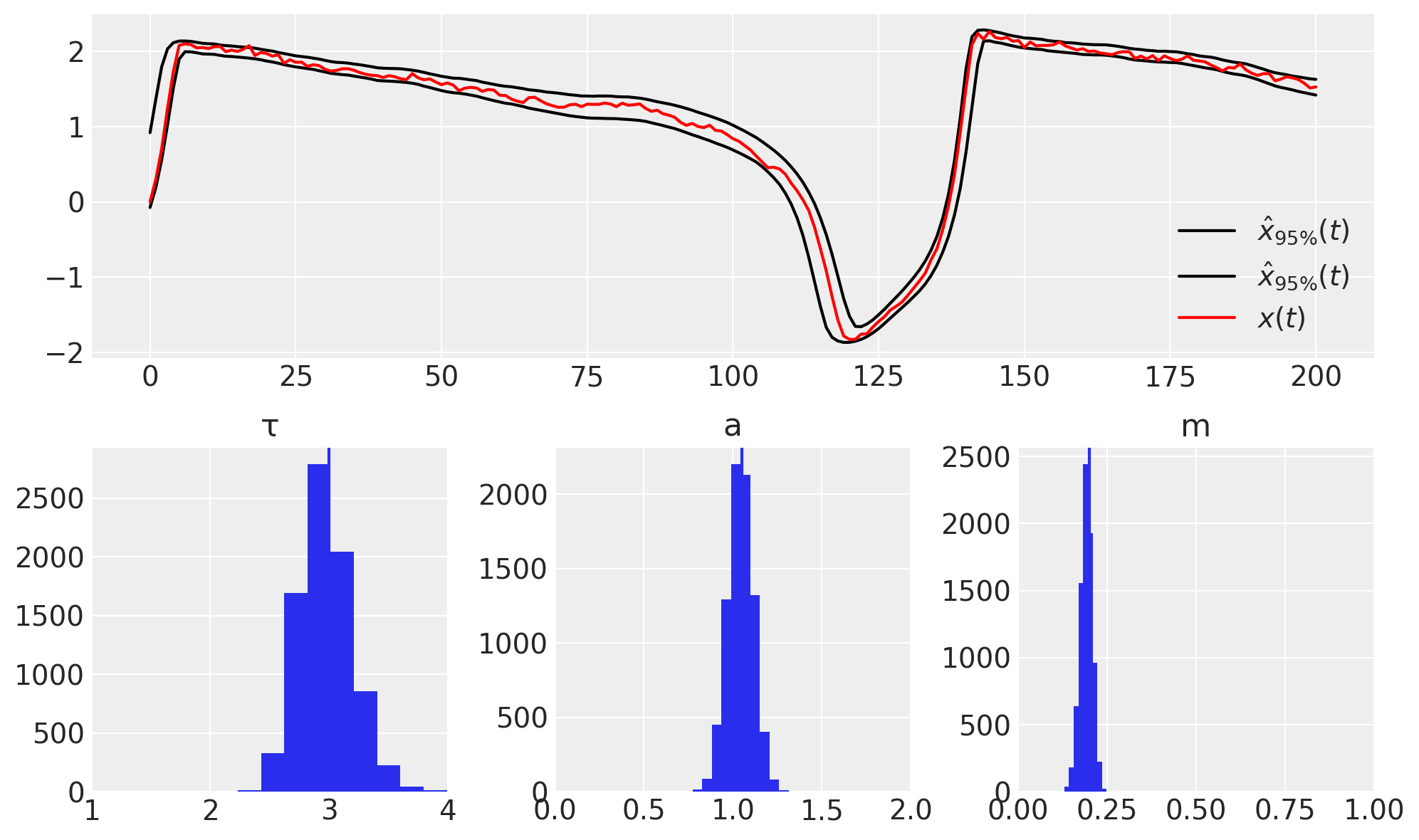
figure(figsize=(10, 6))
subplot(211)
plot(percentile(trace[xyh][..., 0], [2.5, 97.5], axis=0).T, "k", label=r"$\hat{x}_{95\%}(t)$")
plot(xs, "r", label="$x(t)$")
legend(loc=0)
subplot(234), hist(trace["τh"]), axvline(τ), xlim([1.0, 4.0]), title("τ")
subplot(235), hist(trace["ah"]), axvline(a), xlim([0, 2.0]), title("a")
subplot(236), hist(trace["mh"]), axvline(m), xlim([0, 1]), title("m")
tight_layout()

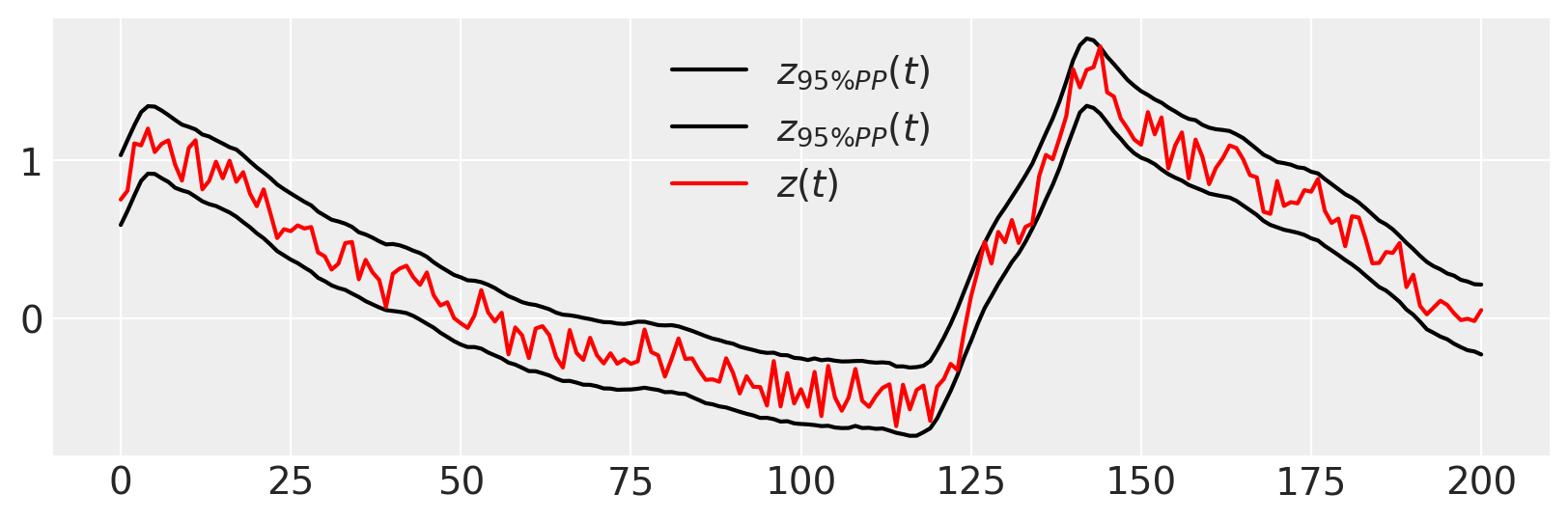
Again, we can perform a posterior predictive check, that our data are likely given the fit model

# generate trace from posterior
ppc_trace = pm.sample_posterior_predictive(trace, model=model)

# plot with data
figure(figsize=(10, 3))
plot(percentile(ppc_trace["zh"], [2.5, 97.5], axis=0).T, "k", label=r"$z_{95\% PP}(t)$")
plot(zs, "r", label="$z(t)$")
legend()

100.00% [8000/8000 00:12<00:00]

<matplotlib.legend.Legend at 0x7f8da12af490>

%load_ext watermark
%watermark -n -u -v -iv -w

scipy            1.4.1
logging          0.5.1.2
matplotlib.pylab 1.18.5
re               2.2.1
pymc3            3.9.0
matplotlib       3.2.1
numpy            1.18.5
arviz            0.8.3
last updated: Mon Jun 15 2020 

CPython 3.7.7
IPython 7.15.0
watermark 2.0.2