%load_ext autoreload
%autoreload 2

import os

os.environ["THEANO_FLAGS"] = "floatX=float64"

import logging

import arviz
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
import theano
import theano.tensor as tt

from scipy.integrate import odeint

# this notebook show DEBUG log messages
logging.getLogger("pymc3").setLevel(logging.DEBUG)

import IPython.display

pymc3.ode: Shapes and benchmarking

Demo Scenario: Simple enzymatic reaction

The model has two ODEs with 3 parameters in total.

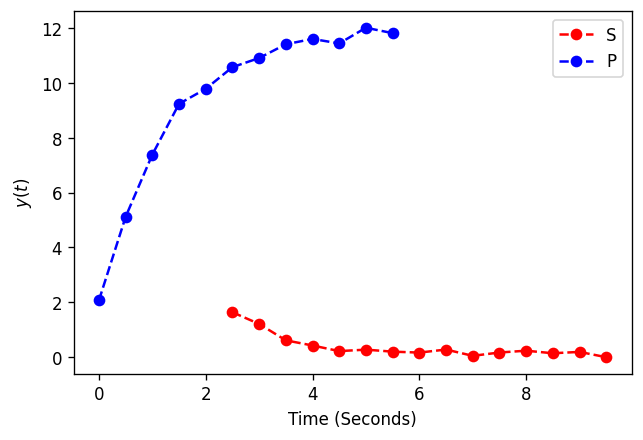
In our generated data, we’ll observe S and P at different times to demonstrate how to slice in such cases.

# For reproducibility
np.random.seed(23489)


class Chem:
    @staticmethod
    def reaction(y, t, p):
        S, P = y[0], y[1]
        vmax, K_S = p[0], p[1]
        dPdt = vmax * (S / K_S + S)
        dSdt = -dPdt
        return [
            dSdt,
            dPdt,
        ]


# Times for observation
times = np.arange(0, 10, 0.5)
red = np.arange(5, len(times))
blue = np.arange(12)
x_obs_1 = times[red]
x_obs_2 = times[blue]

y0_true = (10, 2)
theta_true = vmax, K_S = (0.5, 2)
sigma = 0.2

y_obs = odeint(Chem.reaction, t=times, y0=y0_true, args=(theta_true,))
y_obs_1 = np.random.normal(y_obs[red, 0], sigma)
y_obs_2 = np.random.normal(y_obs[blue, 1], sigma)

fig, ax = plt.subplots(dpi=120)
plt.plot(x_obs_1, y_obs_1, label="S", linestyle="dashed", marker="o", color="red")
plt.plot(x_obs_2, y_obs_2, label="P", linestyle="dashed", marker="o", color="blue")
plt.legend()
plt.xlabel("Time (Seconds)")
plt.ylabel(r"$y(t)$")
plt.show()

# To demonstrate that test-value computation works, but also for debugging
theano.config.compute_test_value = "raise"
theano.config.exception_verbosity = "high"
theano.config.traceback.limit = 100

def get_model():
    with pm.Model() as pmodel:
        sigma = pm.HalfCauchy("sigma", 1)
        vmax = pm.Lognormal("vmax", 0, 1)
        K_S = pm.Lognormal("K_S", 0, 1)
        s0 = pm.Normal("red_0", mu=10, sigma=2)

        y_hat = pm.ode.DifferentialEquation(
            func=Chem.reaction, times=times, n_states=len(y0_true), n_theta=len(theta_true)
        )(y0=[s0, y0_true[1]], theta=[vmax, K_S], return_sens=False)

        red_hat = y_hpt.T[0][red]
        blue_hat = y_hpt.T[1][blue]

        Y_red = pm.Normal("Y_red", mu=red_hat, sigma=sigma, observed=y_obs_1)
        Y_blue = pm.Normal("Y_blue", mu=blue_hat, sigma=sigma, observed=y_obs_2)

    return pmodel


def make_benchmark():
    pmodel = get_model()

    # select input variables & test values
    t_inputs = pmodel.cont_vars
    # apply transformations as required
    test_inputs = (np.log(0.2), np.log(0.5), np.log(1.9), 10)

    # create a test function for evaluating the logp value
    print("Compiling f_logpt")
    f_logpt = theano.function(
        inputs=t_inputs,
        outputs=[pmodel.logpt],
        # with float32, allow downcast because the forward integration is always float64
        allow_input_downcast=(theano.config.floatX == "float32"),
    )
    print(f"Test logpt:")
    print(f_logpt(*test_inputs))

    # and another test function for evaluating the gradient
    print("Compiling f_logpt")
    f_grad = theano.function(
        inputs=t_inputs,
        outputs=tt.grad(pmodel.logpt, t_inputs),
        # with float32, allow downcast because the forward integration is always float64
        allow_input_downcast=(theano.config.floatX == "float32"),
    )
    print(f"Test gradient:")
    print(f_grad(*test_inputs))

    # make a benchmarking function that uses random inputs
    # - to avoid cheating by caching
    # - to get a more realistic distribution over simulation times
    def bm():
        f_grad(
            np.log(np.random.uniform(0.1, 0.2)),
            np.log(np.random.uniform(0.4, 0.6)),
            np.log(np.random.uniform(1.9, 2.1)),
            np.random.uniform(9, 11),
        )

    return pmodel, bm

model, benchmark = make_benchmark()

print("\nPerformance:")
%timeit benchmark()

Applied log-transform to sigma and added transformed sigma_log__ to model.
Applied log-transform to vmax and added transformed vmax_log__ to model.
Applied log-transform to K_S and added transformed K_S_log__ to model.
make_node for inputs -5657601466326543627

Compiling f_logpt
Test logpt:
[array(5.73420592)]
Compiling f_logpt

grad w.r.t. inputs -5657601466326543627

Test gradient:
[array(-12.25120609), array(26.04782273), array(-9.38484546), array(11.26454126)]

Performance:
23.7 ms ± 429 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Inspecting the computation graphs

If you zoom in to the large DifferentialEquation ellipse in the top, you can follow the blue arrows downwards to see that the gradient is directly passed from the original DifferentialEquation Op node.

theano.printing.pydotprint(tt.grad(model.logpt, model.vmax), "ODE_API_shapes_and_benchmarking.png")
IPython.display.Image("ODE_API_shapes_and_benchmarking.png")

grad w.r.t. inputs -5657601466326543627

The output file is available at ODE_API_shapes_and_benchmarking.png

With the cell below, you can visualize the computation graph interactively. (The HTML file is saved next to this notebook.)

If you need to install graphviz/pydot, you can use these commands:

conda install -c conda-forge python-graphviz
pip install pydot

from theano import d3viz

d3viz.d3viz(model.logpt, "ODE_API_shapes_and_benchmarking.html")

%load_ext watermark
%watermark -n -u -v -iv -w

numpy   1.18.5
pymc3   3.9.0
theano  1.0.4
logging 0.5.1.2
IPython 7.15.0
arviz   0.8.3
last updated: Sat Jun 13 2020 

CPython 3.7.7
IPython 7.15.0
watermark 2.0.2