BetaNegativeBinomial#

class pymc_experimental.distributions.BetaNegativeBinomial(name, alpha, beta, r, **kwargs)[source]#

Beta Negative Binomial distribution.

The pmf of this distribution is

\[f(x \mid \alpha, \beta, r) = \frac{B(r + x, \alpha + \beta)}{B(r, \alpha)} \frac{\Gamma(x + \beta)}{x! \Gamma(\beta)}\]

where \(B\) is the Beta function and \(\Gamma\) is the Gamma function.

For more information, see https://en.wikipedia.org/wiki/Beta_negative_binomial_distribution.

(Source code, png, hires.png, pdf)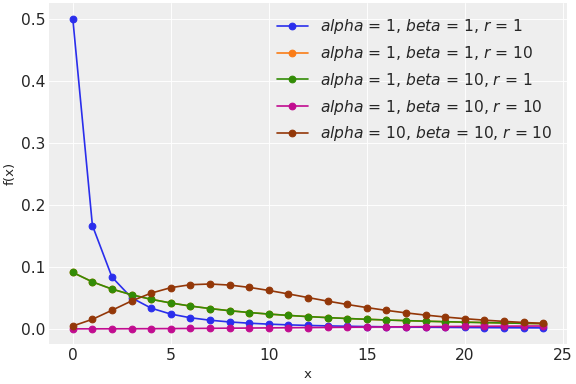

../_images/pymc_experimental-distributions-BetaNegativeBinomial-1.png

Support

\(x \in \mathbb{N}_0\)

Mean

\({\begin{cases}{\frac {r\beta }{\alpha -1}}&{\text{if}}\ \alpha >1\\\infty &{\text{otherwise}}\ \end{cases}}\)

Variance

\({\displaystyle {\begin{cases}{\frac {r\beta (r+\alpha -1)(\beta +\alpha -1)}{(\alpha -2){(\alpha -1)}^{2}}}&{\text{if}}\ \alpha >2\\\infty &{\text{otherwise}}\ \end{cases}}}\)
Parameters:

  • alpha (tensor_like of float) – shape of the beta distribution (alpha > 0).

  • beta (tensor_like of float) – shape of the beta distribution (beta > 0).

  • r (tensor_like of float) – number of successes until the experiment is stopped (integer but can be extended to real)

__init__()#

Methods

__init__()

beta_negative_binomial_dist(alpha, beta, r, size)

beta_negative_binomial_logp(value, alpha, ...)

dist(alpha, beta, r, **kwargs)